Простейшая пожизненная рента пренумерандо описывается следующим образом: начиная с момента времени 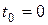 , человек один раз в начале каждого года начинает получать определенную постоянную сумму, которую примем в качестве единицы измерения денежных сумм. Выплаты этой суммы производятся только во время жизни человека, что и отличает эту страховую ренту от постоянных рент, рассмотренных в финансовой математике.
, человек один раз в начале каждого года начинает получать определенную постоянную сумму, которую примем в качестве единицы измерения денежных сумм. Выплаты этой суммы производятся только во время жизни человека, что и отличает эту страховую ренту от постоянных рент, рассмотренных в финансовой математике.
Обозначим через х возраст человека в момент времени 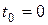 начала платежей. Тогда выплаты будут производиться в моменты времени
начала платежей. Тогда выплаты будут производиться в моменты времени 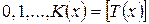 , где
, где 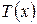 - остаточная продолжительность жизни. То есть имеем дело с годовой рентой пренумерандо со случайным числом выплат
- остаточная продолжительность жизни. То есть имеем дело с годовой рентой пренумерандо со случайным числом выплат 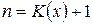 . Найдем современную стоимость такой ренты
. Найдем современную стоимость такой ренты
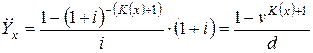 , (1)
, (1)
которая является случайной величиной. Здесь 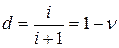 - годовая ставка дисконтирования.
- годовая ставка дисконтирования.
Так как 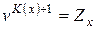 - современная стоимость полного дискретного страхования жизни, то
- современная стоимость полного дискретного страхования жизни, то
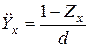 , (2)
, (2)
поэтому расчет характеристик пожизненной ренты можно свести к расчету характеристик соответствующего дискретного страхования жизни.
Найдем актуарную современную стоимость пожизненной ренты (нетто-премию):
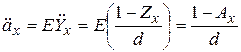 , (3)
, (3)
или
 . (4)
. (4)
Для расчета защитной надбавки 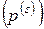 и оценки вероятности разорения компании необходимо уметь вычислять и дисперсию
и оценки вероятности разорения компании необходимо уметь вычислять и дисперсию 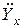 , а именно
, а именно
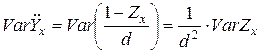 , (5)
, (5)
где 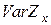 вычисляется так же, как и в предыдущей главе.
вычисляется так же, как и в предыдущей главе.
Формула (4) получена нами так называемым методом суммарной выплаты, когда пожизненная рента рассматривается как сумма случайного числа 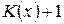 детерминированных слагаемых. Можно применить и другой метод – метод текущего платежа, который рассматривает эту ренту как сумму детерминированного числа случайных слагаемых.
детерминированных слагаемых. Можно применить и другой метод – метод текущего платежа, который рассматривает эту ренту как сумму детерминированного числа случайных слагаемых.
Отметим также, что если при страховании рент речь пойдет о ренте постнумерандо, когда страховые выплаты будут производиться в конце соответствующего периода, то вычисление современной стоимости будет производиться по формуле:
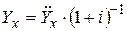 .
.
№ 14. Вычислите актуарную стоимость полной пожизненной ренты, выплачиваемой раз в год в начале года в размере 10000 руб., если годовая процентная ставка равна 20%. Возраст человека на момент заключения договора страхования – 30 лет, а продолжительность жизни описывается моделью де Муавра с предельным возрастом 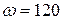 лет.
лет.
Решение. Воспользуемся формулой (3):
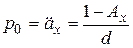 ,
,
где
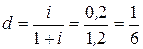 ,
, 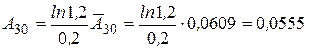 .
.
Следовательно,
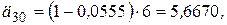
или в рублях это составит величину:
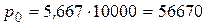 руб.
руб.
Ответ: 56670 руб.
 2015-07-04
2015-07-04 1703
1703
