ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №12
1. Структурная схема лабораторной САП представлена на рис. 12.1.

Рисунок 12.1 – Структурная схема лабораторной САП
Необходимо записать передаточные функции элементов для линейной САП, взяв в качестве передаточной функции электродвигателя следующую:
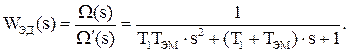
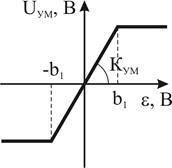
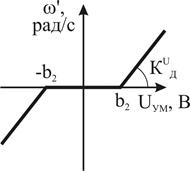
2. Бригады, сидящие за стендами с нечетными номерами в качестве нелинейного элемента используют усилитель мощности, а с четными номерами – электродвигатель СЛ-267. Внешний вид нелинейностей и их параметры приведены на рис. 8.2(а, б) соответственно.
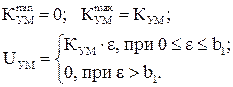
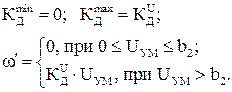
а) б)
Рисунок 12.2 – Характеристики нелинейных элементов
(а – усилителя мощности, б – электродвигателя)
Общее выражение для гармонически линеаризованной нелинейной функции (результат разложения в ряд Фурье):
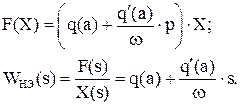
Допущение: характеристики симметричны относительно начала координат. С учетом принятого допущения, для симметричной однозначной нелинейности 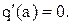
Для усилителя мощности:
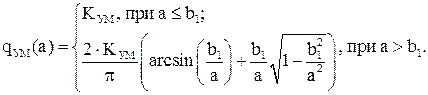
Для электродвигателя:
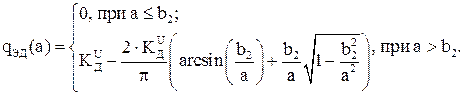
Необходимо построить графики зависимостей q(a) для электродвигателя и усилителя мощности (рис. 12.3), подставляя в соответствующие выражения значения a и b.
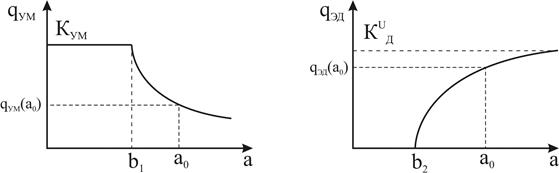
Рисунок 12.3 – Схематические изображения графиков зависимостей q(a)
3. Записать передаточную функцию замкнутой САП с учетом гармонически линеаризованной нелинейности:
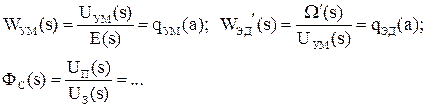
4. Определить частоту и амплитуду автоколебаний в исходной системе.
Для этого используется характеристическое уравнение:
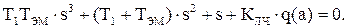
Частотное характеристическое уравнение получаем, выполнив подстановку 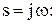
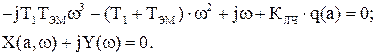
Записать выражения для действительной и мнимой частей частотного характеристического уравнения, приравнять их нулю и из полученных уравнений выразить 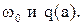 По графику функции
По графику функции 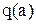 найти
найти 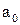 , как показано на рис. 12.3.
, как показано на рис. 12.3.
Из выражения для 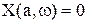 находим значение граничного коэффициента передачи линейной части системы
находим значение граничного коэффициента передачи линейной части системы 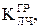 при
при 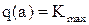 .
.
5. Выполнить построение графика границы автоколебаний (рис. 12.4).
Для этого необходимо для 5-6 значений 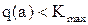 рассчитать значения коэффициента передачи линейной части КЛЧ.
рассчитать значения коэффициента передачи линейной части КЛЧ.
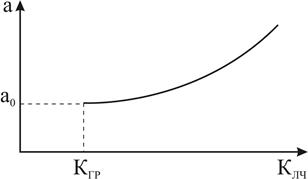
Рисунок 12.4 – Схематическое изображение графика границы автоколебаний
6. Произвести проверку, для чего при трех значениях КЛЧ (КЛЧ1<КГР, КЛЧ2=КГР, КЛЧ3>КГР,) методом Гурвица оценить устойчивость замкнутой САП.
 2015-07-04
2015-07-04 351
351







