2015-07-21
947
1°. (AB) C = A (BC) – ассоциативность.
Это свойство надо формулировать так: если определены произведения матриц AB и (AB) C, то определены и произведения BC и A (BC), причем (AB) C = A (BC).
2°. A (B + C) = AB + AC – дистрибутивность умножения относительно сложения.
3°. (a A) B = A (a B) = a(AB).
4°. EA = A; AE = A.
Докажем первое свойство, остальные сформулируйте текстом и докажите самостоятельно – в качестве упражнения. Итак, доказательство ассоциативности:
►Пусть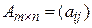 
. Так как существует произведение АВ, то 
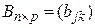, значит, 
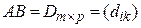. Так как существует произведение 
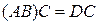, то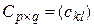 
, тогда 
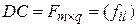. А значит, произведение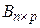 
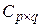определено. Пусть 
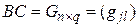. Тогда определено и произведение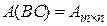 
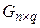
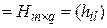. Таким образом, мы видим, что размеры матриц 
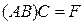и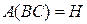 
совпадают, и для доказательства равенства этих матриц остается доказать равенство их соответствующих элементов. Приступаем к вычислениям:
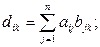
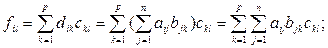(1.5)
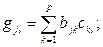
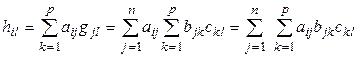. (1.6)
На основании леммы 1.1, сравнивая (1.5) и (1.6), получаем
: 
,
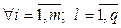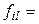
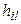и поэтому F = H. ◄
