Иногда по разным причинам матрицу удобно разбить на блоки. Полученная матрица, элементами которой являются опять же матрицы, называется блочной. Например, матрица В разбита на 4 блока, а матрица С – на 6:
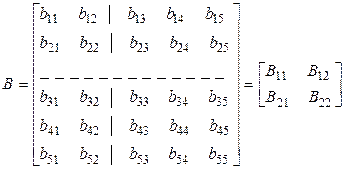 ,
,
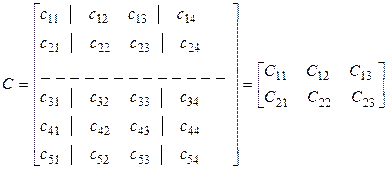 .
.
Заметим, что если 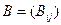 − блочная матрица, то все её элементы − матрицы
− блочная матрица, то все её элементы − матрицы 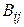 − при фиксированном i имеют одинаковое число строк, а при фиксированном j − одинаковое число столбцов.
− при фиксированном i имеют одинаковое число строк, а при фиксированном j − одинаковое число столбцов.
Если матрицы имеют одинаковые размеры и разбиты на блоки одинаковым образом, то их можно складывать по тому же принципу, что и обычные. Обычным образом блочные матрицы умножаются и на число.
Умножаются блочные матрицы формально также как обычные. Пусть 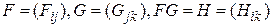 . Тогда
. Тогда
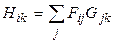 .
.
При этом необходимо, чтобы существовали все произведения 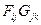 . Например, запишем по такому правилу произведение приведенных блочных матриц В и С:
. Например, запишем по такому правилу произведение приведенных блочных матриц В и С:
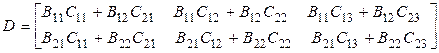 .
.
Убедимся в том, что в действительности 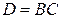 . Посчитаем для проверки элемент
. Посчитаем для проверки элемент 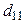 . Чтобы его найти, следует сложить элементы матриц
. Чтобы его найти, следует сложить элементы матриц 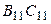 и
и 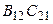 , расположенные в первой строке и первом столбце. Итак,
, расположенные в первой строке и первом столбце. Итак,
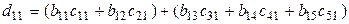 ,
,
что действительно совпадает с соответствующим элементом матрицы 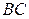 . Аналогично проверяется равенство остальных элементов.
. Аналогично проверяется равенство остальных элементов.
Для блочных матриц легко задается и операция транспонирования. Например,
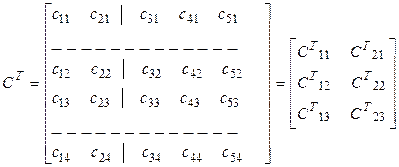 ,
,
т. е. блочная матрица транспонируется так же, как и обычная, только все её элементы также заменяются на транспонированные.
Блочную матрицу 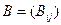 будем называть блочно-диагональной, если при
будем называть блочно-диагональной, если при 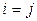 матрицы
матрицы 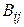 являются квадратными, их главные диагонали расположены на главной диагонали матрицы В, а при
являются квадратными, их главные диагонали расположены на главной диагонали матрицы В, а при 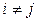
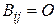 . В этом случае нет необходимости нумеровать диагональные блоки двумя индексами, достаточно одного. Блочно-диагональную матрицу с блоками
. В этом случае нет необходимости нумеровать диагональные блоки двумя индексами, достаточно одного. Блочно-диагональную матрицу с блоками 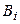 на главной диагонали будем обозначать так:
на главной диагонали будем обозначать так: 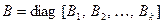 .
.
 2015-07-21
2015-07-21 3682
3682








