Определение. Матрица 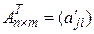 называется транспонированной к матрице
называется транспонированной к матрице 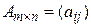 , если
, если
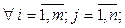
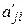
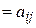 .
.
Таким образом, из определения видим, что при транспонировании матрицы строки становятся столбцами и наоборот. Например, если
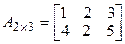 , то
, то 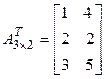 .
.
Кроме обозначения AT для матрицы, транспонированной к А, используют еще и следующие: 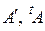 .
.
Свойства операции транспонирован ия
1°. 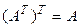 .
.
2°. 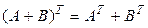 .
.
3°. 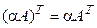 .
.
4°. 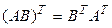 .
.
Первые три свойства практически очевидны. Докажем четвертое, которое формулируется так: если определено произведение матриц АВ, то определено и произведение 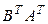 , причем
, причем
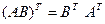 . (1.7)
. (1.7)
►Пусть 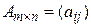 . Так как определено произведение АВ, то В имеет размеры
. Так как определено произведение АВ, то В имеет размеры 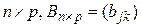 ,
, 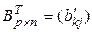 ,
, 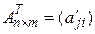 , а значит, определено произведение
, а значит, определено произведение 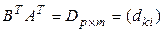 . Обозначим
. Обозначим 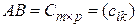 , тогда
, тогда 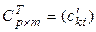 . Как видим, матрицы
. Как видим, матрицы 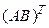 и
и 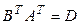 из левой и правой частей равенства (1.7) имеют одинаковые размеры, и для доказательства их равенства остается доказать равенство соответствующих элементов.
из левой и правой частей равенства (1.7) имеют одинаковые размеры, и для доказательства их равенства остается доказать равенство соответствующих элементов.
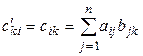 , (1.8)
, (1.8)
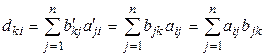 . (1.9)
. (1.9)
Сравнивая (1.8) и (1.9), видим, что 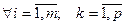
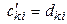 .◄
.◄
 2015-07-21
2015-07-21 1410
1410
