Если А – квадратная матрица, то определено произведение АА, которое называется квадратом матрицы А и обозначается А 2. Квадрат матрицы А является квадратной матрицей того же порядка, что и А, поэтому определено и произведение АА 2. Вообще, если для квадратной матрицы определена степень 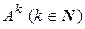 , то по определению
, то по определению 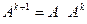 .
.
Лемма 1.2. Для любой квадратной матрицы А и для любого натурального n справедливо равенство 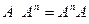 .
.
►Доказательство проведем методом математической индукции.
Проверяем утверждение при n = 1: А А = A A – истинно.
Предполагая, что утверждение верно при n = k, доказываем, что оно верно при n = k +1.
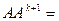 [определение k + 1-й степени] =
[определение k + 1-й степени] = 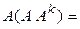 [предположение индукции] =
[предположение индукции] = 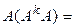 [ассоциативность произведения] =
[ассоциативность произведения] = 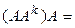 [определение k + 1-й степени] =
[определение k + 1-й степени] = 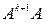 .◄
.◄
Если произведение матриц коммутативно, то они называются коммутирующими или перестановочными. Таким образом, степени одной и той же квадратной матрицы перестановочны.
Можно доказать, что натуральные степени квадратной матрицы обладают следующими свойствами:
1°. 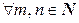 :
: 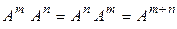 ;
;
2°. 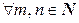 :
: 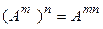 .
.
Если 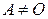 , то по определению считается, что A 0 = E.
, то по определению считается, что A 0 = E.
 2015-07-21
2015-07-21 2407
2407








