Задача №5

Написати формули переходу від репера 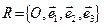до репера 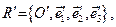якщо , , , .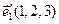

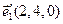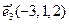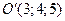Розвязання:

Формули переходу від репера 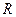до репера 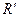мають вигляд:

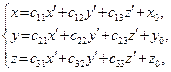
де 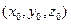координати 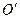, 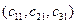координати 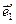, 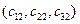координати 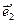, 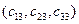координати .

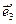Підставивши відповідні значення отримаємо:

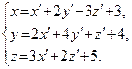
Задачі для самостійної роботи.

1) На осі ординат визначити точку, рівновіддалену від точок , .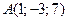

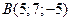2) Дано вершини трикутника 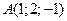, , 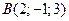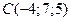. Обчислити довжину бісектриси його внутрішнього кута при вершині .

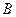3) Дано три вершини паралелограма 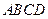: 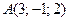, , 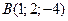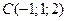. Знайдіть координати його четвертої вершини .

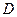4) Дано вершини трикутника 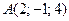, , 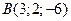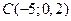. Обчислити довжину медіани, яка проведена із вершини .

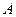5) Дано дві вершини 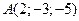, 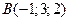паралелограма 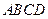і точка перетину його діагоналей 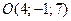. Визначити дві інші вершини паралелограма.

6) Визначити відношення у якому кожна з координатних площин поділяє відрізок : , .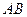

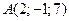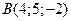7) Довести, що відрізки, які сполучають середини протилежних ребер тетраедра, перетинаються в одній точці і діляться в ній пополам.

8) Дано тетраедр 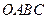. Написати формули переходу від репера 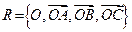до репера .

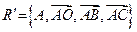Рекомендована література

1. Конспект лекцій.

2. Яковець В.П. Аналітична геометрія / В.П.Яковець,В.Н. Боровик, Л.В.Ваврикович.-Суми, Університетська книга, 2004.-304 с. р.

3. Гринів Б.В. Аналітична геометрія / Б.В.Гринів, І.К.Кириченко.- Харків, Гімназія, 2008.-340 с.

4. Боровик В.Н.Курс вищої геометрії / В.Н.Боровик, В.П. Яковець.- Суми, Університетська книга, 2010.-360с