Выборочные оценки характеристик случайных величин

Различные статистические оценки выборки являются выборочными оценками соответствующих характеристик случайной величины.

Выборочное среднее (обозначается как М или ) является оценкой математического ожидания и определяется как среднее арифметическое всех элементов выборки:

M = .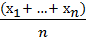

Выборочное среднее можно также выразить через частоты различных элементов выборки:

M = p₁x₁ + … + p_nx_n,

где в суммировании участвуют только различные значения х_і.

Выборочное среднее обладает тем свойством, что сумма отклонений всех наблюдений от этого числа равна 0, т. е. наблюдения превышающие среднее, уравновешиваются наблюдениями, значения которых ниже среднего.

Пример 5. Для выборки, состоящей из 8 значений: 1, 1, 3, 4, 8, 9, 10, 12 среднее равно (1 + 1+ 3 + 4 + 8 + 9+10+ 12)/8 = 48/8 = 6.

Важную роль при анализе связей между переменными играет сумма квадратов отклонений наблюдений от среднего (обозначается как SS):

SS = (x₁ –M)² + …+ (x_n – M)²

В практических расчетах удобно пользоваться другим выражением суммы квадратов (получаемым из исходного путем тождественных преобразований):

SS = (x₁² – 2M x₁ M²) + … + (x_n²- 2M x_n M²) = (x₁² + … + x_n²) – 2M (x₁ + … + x_n) + nM² =

= (x₁² + … + x_n²) - nM².

Выборочной оценкой дисперсии (обозначается как S², σ²) является сумма квадратов отклонений, деленная на число наблюдений за вычетом 1:

S² = .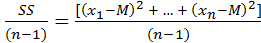

Эта оценка дисперсии является несмещенной (т. е. ее математическое ожидание совпадает с истинным значением дисперсии случайной величины). Иногда в качестве выборочной оценки дисперсии используют величину SS /п. В теории статистического оценивания доказывается, что эта оценка является смещенной, поэтому предпочтительнее пользоваться оценкой, приведенной выше. В различных компьютерных системах анализа данных, начиная от калькуляторов со встроенными статистическими функциями, реализованы различные варианты оценки дисперсии — смещенная или несмещенная (в некоторых случаях обе), на что следует обращать внимание.

Среднеквадратичное (стандартное) отклонение среднего (обозначается как S, σ) определяется как квадратный корень из дисперсии:

S = .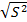

Пример 6. Для выборки из примера 5.

SS = (1 – 6)² + (1 - 6)² + (3 – 6)² + (4 – 6)² + (8 – 6)² + (9 – 6)² + (10 – 6)² + (12 – 6)² =

= (-5)² + (-5)² + (-3)² +2² + 2² +3² + 4² + 6² = 128,

S² = SS/7 = 18,29

S = 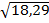= 4,28

Выборочное среднее чувствительно к «экстремальным» значениям, сильно отклоняющимся от остальных значений выборки. Тем более чувствительны к появлению нетипичных для выборки значений оценки, характеризующие рассеяние относительно среднего.

Пример 7. Если бы в вариационном ряду из примера 5 последнее значение составляло не 12, а 42, то выборочное среднее равнялось бы 9,75 (т.е. увеличилось бы на 22%), а стандартное отклонение — 13,5 (увеличение более чем в 3 раза).

Вышеупомянутая ситуация иллюстрирует тот факт, что на практике всегда полезно внимательно относиться к первичным данным и прежде чем использовать математические алгоритмы статистического анализа, оценивать визуально их качество, наличие «экстремальных» отклонений, возможность возникновения артефактов и в соответствии с этим принимать решение о том, стоит ли осуществлять статистическую обработку или, может быть, повторить эксперимент. Иногда в таких случаях отбрасываются крайние значения выборки и дальнейший анализ производится без них, но это решение должно быть осознанным и обоснованным.

При описании экспериментальных данных в литературе нередко приводится такая характеристика, как стандартная ошибка среднего (обычно обозначается как т, а диапазон значений среднего с учетом ошибки указывается в виде М±т). Стандартная ошибка среднего определяется как стандартное отклонение, деленное на корень квадратный из числа наблюдений:

M = .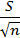

Эта величина, в отличие от всех других рассматриваемых в данном пункте оценок, не является оценкой какого-либо из параметров распределения случайной величины, но характеризует точность оценки среднего по имеющимся данным. Стандартная ошибка среднего зависит от числа наблюдений: с увеличением числа испытаний она уменьшается (до сколь угодно малых величин при достаточно больших п). Приведенная выше формула для оценки стандартной ошибки среднего справедлива только для нормального распределения.

Медианой выборки называется число, для которого количество наблюдений, превышающих его, равно количеству наблюдений, меньших его. Для определения медианы выборка должна быть упорядочена по возрастанию. Если число наблюдений нечетно, за медиану принимается средний по порядку элемент вариационного ряда, а если чётно — среднее арифметическое между двумя ближайшими друг к другу значениями вариационного ряда, равноудаленными от его начала и конца. Выборочные квартили определяются как числа, разбивающие вариационный ряд на 4 группы с одинаковым числом наблюдений. Для выборок с большим (в несколько сотен) числом наблюдений аналогичным образом можно определить и квантили.

Медиана более устойчива к появлению в выборке экстремальных значений, чем выборочное среднее.

Пример 8. Для выборки из примера 5 медиана равна 5-му значению вариационного ряда, т. е. 8. При замене последнего значения вариационного ряда с 12 на 42 медиана не изменяется.

Выборочной модой для дискретной случайной величины называется такое значение x_k, частота появлений которого в выборке больше, чем для любых других значений. Выборка может иметь более чем одну моду. В случае непрерывной случайной величины моду определяют кик середину интервала, в который попало наибольшее число наблюдений. Результаты определения моды в этом случае зависят от выбора числа интервалов.

Мода, в отличие от медианы и среднего, очень чувствительна не к экстремальным, а к типичным для данной выборки значениям. Поэтому определять выборочную моду имеет смысл только при очень больших (порядка нескольких сотен) объемах выборок.

Пример 9. Для выборки из примера 5 мода равна 1. При изменении 6-го значения с 9 на 10 появилась бы вторая мода, равная 10, тогда как медиана выборки не изменилась бы, а среднее увеличилось бы незначительно (на 0,125).

Выборочное среднее, медиана и мода служат оценками положения центра распределения. Для количественных переменных могут быть вычислены все три оценки. Соотношения между этими оценками несут важную информацию о виде распределения (совпадение медианы и среднего свидетельствует о симметричности распределения, наличие неединственной моды — о неоднородности выборки), поэтому при описании экспериментальных данных имеет смысл вычислять их все.

Для качественных переменных единственной возможной характеристикой центрального положения распределения является мода.

Пример 10. Из 100 обследованных группы крови О, А, В и АВ имели, соответственно, 43, 30, 18 и 9 человек. Следовательно, модальной для данной выборки является группа крови О.

Для порядковых переменных основным показателем центра распределения также является мода. Вычисление среднего и медианы формально возможно, но, вообще говоря, некорректно, поскольку результатами таких вычислений могут оказаться числа, не принадлежащие к множеству допустимых значений дискретной случайной величины (например, дробные, тогда как дискретным величинам приписывают как правило, только целочисленные значения). Тем не менее, и в этом случае определение медианы как границы, разбивающей выборку на две равночисленные подгруппы, может оказаться полезным. В случае, если значение медианы не совпадает ни с одним из уровней полуколичественной переменной, она показывает, между какими уровнями проходит такая граница.

Если интервалы между соседними значениями ординальной переменной равномерны, допустимо и вычисление среднего. В этом случае величина среднего показывает не только между какими соседними значениями находится средневероятное выборочное значение, но и к какому из этих значений она ближе.

Решая вопрос о том, следует ли вычислять и приводить среднее значение для переменных, измеряемых в балльных шкалах, необходимо уточнять, является ли шкала равномерной. В некоторых случаях (особенно в психологических исследованиях) градуировку шкал специально производят не из соображений равномерности шкалы, а так, чтобы она соответствовала разбиению населения на равночисленные группы (например, 5-балльная шкала строится таким образом, чтобы каждому ее уровню соответствовало 20 % населения). Встречается также градуировка шкалы в фиксированных долях от стандартного отклонения (которое определяется по достаточно большой группе, для которой подтверждена валидность теста).

Пример 11. В табл. 4.1 приведены результаты опроса, проведенного среди двух одинаковых по численности, половому и возрастному составу и социально- экономическому статусу групп населения, проживающих на территориях, одна из которых характеризуется высоким уровнем загрязнения воды и почвы.

Качественным градациям состояния здоровья можно сопоставить оценки но 5-балльной шкале (приведенные в таблице в скобках), причем эту шкалу можно считать более или менее равномерной. Тогда возможно вычислить оценки положения центра распределения для обеих групп. Модальное значение оценки для обеих групп равно 3. Медианы обеих групп также совпадают и равны 3 (50-е и 51-е значение вариационного ряда в обоих случаях соответcтвуют этой величине оценки). Различия распределения оценок в двух группах проявляются только в различии средних:

для первой группы М = 0,02 • 1 + 0,18 • 2 + 0,35 • 3 + 0,29 • 4 + 0,16 • 5 = 0,02 +

+ 0,36 + 1,05 + 1,16 + 0,80 = 3,39;

для второй группы М = 0,12 • 1 + 0,22 • 2 + 0,41 • 3 + 0,19 • 4 + 0,06 • 5 = 0,12 +

+ 0,44 + 1,23 + 0,76 + 0,30 = 2,85.

Таким образом, средневероятное состояние здоровья для жителей незаг рязненной территории находится между удовлетворительным и хорошим, а для загрязненной территории — между плохим и удовлетворительным, т.е. выбо рочное среднее, вычисление которого в данном случае достаточно корректно, оказалось единственной оценкой, улавливающей различия в состоянии здоровья (при данном способе оценки) между территориями с различным уровнем загрязнения.

Таблица 4.1

Результаты самооценки состояния здоровья в двух выборочных группах

Состояние здоровья (субъективная оценка)	Жители незагрязненной территории	Жители загрязненной территории
Очень плохое (1)
Плохое (2)
Удовлетворительное (3)
Хорошее (4)
Очень хорошее (5)
Всего

Все перечисленные выше оценки выборок сводятся к одному числу. Такие оценки называются точечными. К точечным оценкам относятся также такие характеристики рассеяния выборки, как ее размах (разность, между максимальным и минимальным значениями), межквартильный размах (разность между верхней и нижней квартилями), коэффициент вариации (отношение стандартного отклонения к среднему), коэффициент асимметрии. Оценки, состоящие из двух чисел, называются интервальными. К таким оценкам относятся диапазон изменения выборки [ x_min, x_max ] и различные интервалы, связанные с точечными оценками, например, так называемые сигмальные интервалы вида [М - kS, М + kS], где М, S — выборочные оценки среднего и стандартного отклонения, а k — целое число, обычно равное 1, 2 или 3, или же интервалы допустимых значений среднего в видe [М - m, М + m ], где m — стандартная ошибка среднего.

Наиболее распространенная из интервальных оценок выборки — доверительный интервал среднего с заданным доверительным уровнем, т.е. интервал, в котором с заданной вероятностью находится выборочное среднее. В качестве доверительного уровня при оценивании рисков, обусловленных влиянием факторов внешней среды на здоровье, обычно принимается величина 95 %. Чаще всего в качестве доверительного интервала выборочного среднего используется центральный (т. е. симметричный относительно среднего) доверительный интервал среднего, рассчитанный для нормально распределенной случайной величины с параметрами (М, S²), равными, соответственно, выборочному среднему и выборочной дисперсии. В публикациях, если не оговорено иное, под доверительным интервалом подразумевается именно такой интервал. Для нормальной случайной величины 95 %-ный центральный доверительный интервал — это интервал, заключенный между 2,5 %-й и 97,5%-й точками распределения (см. рис. 4.19, 4.20), т.е. интервал [М 1,96S, М + 1,96S]. Чем ближе распределение выборки к нормальному, тем лучше рассчитанный таким образом доверительный интервал характеризует положение центра распределения. Однако для выборок из генеральной совокупности с распределением, сильно отличающимся от нормального, нормальный доверительный интервал не является хорошей оценкой. Например, для асимметрично распределенной выборки, содержащей только положительные значения, нижняя граница нормального доверительного интервала может оказаться отрицательным числом. Такой результат свидетельствует о том, что нормальное распределение плохо аппроксимирует реальное распределение и в качестве интервальной оценки выборки следует использовать другие характеристики, например, интервал между первой и третьей квартилями [Q₁, Q₃], в котором сосредоточена половина значений выборки.

Для порядковых и качественных показателей с малым числом градаций целесообразно приводить целиком таблицы распределения выборки по этим градациям.

Задача 3. В выборочной группе регистрировали следующие показатели:

а) возраст (полных лет);

б) пол;

в) семейное положение;

г) образование;

д) частоту пульса:

д₁) в состоянии покоя

д₂) при выполнении дозированной физической нагрузки;

д₃) при выполнения интеллектуальной нагрузки;

е) результаты заполнения психологического опросника (5 шкал, каждая из которых имеет градации от 1 до 10 баллов);

ж) субъективную оценку конфликтности отношений (конфликтные/нейтральные/хорошие):

ж₁) в семье;

ж₂) на работе;

з) наличие профессиональных вредностей;

и) количество дней болезни за истекший год.

Какие выборочные характеристики целесообразно рассчитывать для каждого из этих показателей и почему? Какая дополнительная информация нужна для оптимального выбора статистических оценок?

Решение. Показатели а), д), и) являются количественными. Для решения вопроса о выборе оптимальных статистических оценок этих показателей необходимо проанализировать характер распределения выборок (например, визуально с помощью гистограмм). Если распределение похоже на нормальное, оптимальными его характеристиками являются среднее и стандартное отклонения. В противном случае, помимо среднего, целесообразно вычислить оценки, наиболее ярко демонстрирующие особенности выборочного распределения — медиану для асимметричных и модальные значения для полимодальных распределений.

Группы показателей е) — порядковые, поэтому для каждого из них необходимо уточнить, является ли шкала измерения равномерной. Если да, то с показателем следует обращаться, как с количественным, если нет — в качестве выборочных характеристик следует определить медиану и моду.

Показатели б), в), ж), з) — качественные с малым числом градаций, поэтому для них следует составить таблицы выборочных частот. Так же следует поступить и с показателем г) — порядковым с малым числом градаций, но для него целесообразно определить и медиану.

4. Статистические гипотезы и критерии

Статистическое решение — это особый способ анализа информации об исследуемых процессах, основанный на учете неопределенностей, неизбежно связанных с регистрацией данных. Поэтому статистические решения всегда имеют вероятностный характер. Именно эта их особенность делает статистические методы оптимальными для анализа рисков.

Процедура принятия статистического решения начинается с формулировки статистической гипотезы, т. е. гипотезы относительно случайных величин, представленных исследуемыми выборками. После этого проверяется, противоречат ли этой гипотезе имеющиеся выборочные данные. Если между гипотезой и данными обнаруживается противоречие, то гипотеза отвергается, если нет — принимается.

Проверка непротиворечивости между гипотезой и выборкой осуществляется с помощью так называемых статистических критериев.

Статистический критерий — это правило, по которому статистическая гипотеза принимается или отвергается в зависимости от значений выборки. Любой статистический критерий делит пространство всевозможных значений выборки на две непересекающиеся области доверительную область, или область принятия гипотезы, т. е. множество значений выборки, при которых гипотеза принимается (точнее, не отвергается), и критическую область, т.е. множество значений, при которых гипотеза отвергается.

Статистические критерии в соответствии с характером проверяемых ими гипотез делятся на два основных класса — параметрические и непараметрические. К первому классу относятся критерии для проверки гипотез, включающих некоторые предположения о виде рас­пределения случайной величины и касающиеся значений параметров этих распределений (например: среднее нормальной случайной величины равно 1; средние двух нормальных случайных величин совпадают; дисперсии двух нормальных выборок различны; две выборки, распределенные по закону Пуассона, имеют одинаковый параметр λ). Непараметрическими называются критерии, не включающие никаких предположений относительно вида распределения исследуемых выборок.

Гипотеза, подлежащая статистической проверке, называется нулевой и обозначается Н₀. Любой статистический критерий строится на использовании какого-либо следствия из факта справедливости нулевой гипотезы. Каждому статистическому критерию соответствует случайная величина, представляющая собой определенную функцию от выборки (например, частное от деления выборочного среднего на стандартную ошибку среднего или число положительных разностей между значениями попарно связанных выборок). Такая случайная величина называется статистикой критерия и обычно носит то же название, что и сам критерий (например, t -статистика для t -критерия Стьюдента, F -статистика для F -критерия Фишера). Любой статистический критерий основан на том, что при условии справедливости нулевой гипотезы статистика критерия имеет определенное распределение, для которого можно построить доверительные области. Поэтому нулевая гипотеза отвергается в том случае, если значение статистики критерия выходит за пре­делы своей доверительной области. Для параметрических критериев распределение статистики критерия при условии выполнения нулевой гипотезы тесно связано с распределением генеральной совокупности, из которой выбираются значения выборки, а для непараметрических - не зависит от вида распределения генеральной совокупности (поэтому непараметрические критерии называются также критериями, свободными от вида распределения). Так например, параметрические критерии сравнения двух выборок основываются на значениях параметров соответствующих распределений, а непараметрические используют тот факт, что две выборки из одной генеральной совокупности имеют одинаковую медиану и вероятности появления значений выше и ниже медианы одинаковы для обеих выборок.

В качестве гипотезы, конкурирующей с нулевой, рассматривается альтернативная гипотеза, обозначаемая H_A. Альтернативы для одной и той же нулевой гипотезы могут быть различными в зависимости от задач исследования. Например, гипотеза о равенстве среднего нормально распределенной случайной величины некоторому заданному числу а может иметь следующие альтернативы:

- среднее равно некоторому числу b ;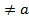

- среднее не равно а (так называемая двухсторонняя альтернатива);

- среднее меньше (больше) а — односторонние альтернативы.

Гипотезы называются простыми, если нулевая и альтернативная гипотезы полностью определяют значение параметра распределения, к которому они относятся (первый из приведенных выше примеров), и сл ожными — в противном случае. Критическая область критерия, с помощью которого проверяется нулевая гипотеза, зависит от вида альтернативной гипотезы. На рис. 4.21 приведены критические области t- критерия Стьюдента, используемого для проверки гипотез о значении среднего нормальной случайной величины (в данном случае — о равенстве среднего нулю) для односторонней и двухсторонней альтернатив.

Ошибкой первого рода называется событие, заключающееся в отклонении нулевой гипотезы при условии, что она верна, а ошибкой второго рода — принятие нулевой гипотезы при условии, что верна альтернативная. Вероятности ошибок первого и второго рода обозначаются буквами α и β. По отношению к статистическому критерию величина α называется уровнем значимости критерия, а величина (1 — α) — доверительным уровнем критерия. В зависимости от выбранной величины α определяется доверительная область статистики критерия. Величина (1 — β) называется мощностью критерия. При проверке статистической гипотезы естественно стремиться к максимальному снижению как α, так и β, однако одновременное снижение этих величин не всегда возможно. На рис. 4.22 изображены критические области и вероятности ошибок α и β для случая, когда нулевая гипотеза заключается в том, что наблюдаемые значения некоторого показателя относятся к нормально распределенной генеральной совокупности с параметрами (a₁, σ₁²), а альтернативная — в том, что параметры распределения равны (a₂, σ₂2). Такая ситуация часто встречается в задачах диагностики по единственному диагностическому показателю, распределение которого у здоровых и больных подчиняется нормальному закону с различными значениями параметров. В таких случаях выбирается критическое значение диагностического показателя х_кр, и обследуемых относят к больным или к здоровым в зависимости от того, выше или ниже критического оказывается индивидуальное значение показателя. Очевидно, что изменение уровня х_кр таким образом, чтобы уменьшить вероятность ошибки первого рода, ведет к росту вероятности ошибки второго рода, и наоборот. На практике оптимальное соотношение уровня значимости и мощности критерия устанавливают, исходя из «цены» последствий ошибки первого и второго рода.

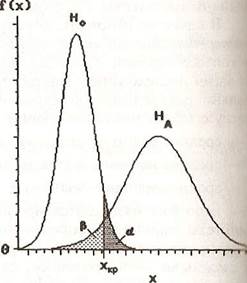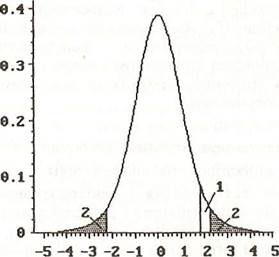
Рис. 4.21. Критические области критерия Рис. 4.22. Ошибки первого и второго

Стьюдента для проверки гипотезы о ра- рода для простой гипотезы о значениях

венстве 0 среднего нормальной случайной параметров нормального распределения

величины:

1 – односторонняя альтернатива;

2 – двухсторонняя альтернатива

Поскольку большая часть параметрических критериев разработана для нормально распределенных случайных величин, одним из первых этапов анализа данных должно быть выяснение нормальности распределения исследуемых выборок. Для этого существуют разнообразные способы. Простейший приблизительный способ — визуальное сравнение выборочной гистограммы с функцией плотности нормального распределения. Количественную оценку соответствия выборочного распреде­ления нормальному можно получить с помощью непараметрических критериев, реализованных во всех статистических пакетах, — крите­рия χ² или критерия Колмогорова—Смирнова. Оба критерия основаны на интервальном разбиении диапазона изменения выборки и срав­нении числа наблюдений в каждом интервале с ожидаемым числом, соответствующим нормальному распределению, среднее и дисперсия которого совпадают с выборочными. Различие между критериями χ² и Колмогорова—Смирнова заключается в том, что первый из них отвергает гипотезу о нормальности выборочного распределения в случае, если слишком велика сумма по всем интервалам отношений квадрата разности между теоретической и реальной частотой к теоретической частоте, а второй — если существует хотя бы один интервал, в котором разность между теоретической и экспериментальной частотами слишком велика. Вследствие такого различия в некоторых случаях эти два критерия дают разные результаты относительно допустимости предположения о нормальности выборочного распределения. Кроме того, результаты использования обоих критериев зависят от субъективного выбора интервального разбиения, поэтому проверка предположения и нормальности распределения с помощью этих формальных критериев дает в принципе не более надежные результаты, чем чисто субъективный анализ гистограммы. Визуальный анализ гистограммы часто оказывается полезным в случае, когда исходная выборка неоднородна, т.е. включает элементы из различных генеральных совокупностей. Неоднородность выборки проявляется в наличии на гистограмме нескольких достаточно сильно удаленных друг от друга пиков частот (например, продолжительность инфекционного заболевания может сильно различаться для вакцинированных и невакцинированных подгрупп населения). Выявление неоднородностей на начальном этапе исследования с последующим анализом причин неоднородности и разбиением исходной выборки на однородные подгруппы позволяет избежать некорректностей, связанных с необоснованным использованием параметрических методов. Кроме того, выделенные подгруппы довольно часто оказываются, в отличие от исходной выборки, нормально распределенными, и поэтому допускают использование всего спектра статистических методов, основанных на предположении о нормальности. Для выборок, распределение которых явно отличается от нормального, следует использовать только методы, свободные от вида распределения.