Дисперсионный анализ

Дисперсионный анализ (английский термин — analysis of variance, сокращенно — ANOVA) при анализе рисков здоровью используется в том случае, если факторы риска регистрируются в порядковых или качественных шкалах, а показатели здоровья — в количественной. Сущность метода сводится к разбиению суммы квадратов отклонений зависимой переменной от своего среднего на несколько компонент, связанных с различными источниками вариабельности — действием отдельных факторов риска, их взаимодействиями — а также остаточную сумму квадратов. Затем суммы квадратов, соответствующие факторам, сопоставляются с остаточной сумой квадратов. Гипотеза о том, что некоторый фактор не оказывает влияния на зависимую переменную, отвергается, если сумма квадратов, соответствующая этому фактору, существенно больше остаточной суммы квадратов. В этом метод дисперсионного анализа сходен с регрессионным. В дисперсионном анализе применяется терминология несколько иная, чем в других разделах статистики: независимые переменные называются факторами, их значения — уровнями фактора, а зависимые переменные — переменными отклика.

Однофакторный дисперсионный анализ используется в случае, когда требуется оценить влияние единственного фактора на переменную отклика. Если имеется I уровней фактора риска, а для i -го уровня фактора — n_i наблюдений переменной отклика у_ij, где индекс j принимает значения от 1 до n_i то средние значения переменной отклика по i-му уровню (обозначаемые как y_i.) выражаются в виде:

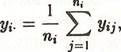а генеральное среднее (обозначаемое как y..) равно

y..=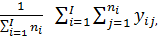

то полную сумму квадратов SS_T можно представить в виде:

SS_T =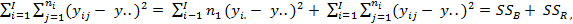

где первая сумма 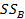называется межгрупповой (она характеризует степень разброса данных между уровнями фактора), а вторая — 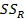— внутригрупповой, или остаточной, поскольку она характеризует разброс данных внутри уровней факторов, обусловленных действием неучтенных факторов и случайных причин.

В качестве нулевой гипотезы в однофакторном дисперсионном анализе рассматривается предложение о равенстве средних переменной отклика для всех уровней фактора. Альтернативой является наличие хотя бы одной пары уровней, для которых средние значения переменной отклика различны.

В теории дисперсионного анализа доказывается, что если нулевая гипотеза верна, то отношение имеет F -распределение Фишера с числами степеней свободы (I — 1), (n — I),

F =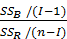

поэтому критической областью при заданном уровне значимости α является область значений F, превышающих квантиль порядка 1 — α распределения Фишера с (I— 1), (n — I) степенями свободы.

Пример 14. В примере 12 каждому значению численности школьников соответствуют два значения частоты заболеваний, поэтому степень влияния численности на частоту заболеваний можно оценить с помощью дисперсионного анализа. Расчеты приведены в табл. 4.6.

у.. = 244/12 = 20,33,

SS_T = 728,67, 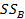= 626,67, 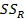= 102,

I = 6, I - 1= 5, п - I = 6,

F_5,6 = =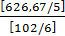

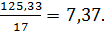
Таблица 4.6

Однофакторный дисперсионный анализ

i	j	yij	yi.	yij - yi.	(yij - yi.)2	yij - yi..	(yij - yi..)2	yi. - yi..	(yi. - yi..)2
			13,5	-1,5	2,25	-8,33	69,44	-6,83	46,69
			13,5	1,5	2,25	-5,33	28,44	-6,82	46,69
			13,5	-2,5	6,25	-9,33	87,11	-6,83	46,69
			13,5	2,5	6,25	-4,33	18,78	-6,83	46,69
	I			-4		-7,33	53,78	-3,33	11,11
						0,67	0,44	-3,33	11,11
			18,5	-1,5	2,25	-3,33	11,11	-1,83	3,36
			18,5	1,5	2,25	-0,33	0,11	-1,83	3,36
				-2		3,67	13,44	5,67	32,11
						7,67	58,78	5,67	32,11
			33,5	-4,5	20,25	8,67	75,11	13,17	173,36
			33,5	4,5	20,25	17,67	312,11	13,17	173,36
Cуммы							728,67		626,67

В таблицах распределения Фишера, имеющихся в любом справочнике по статистике, можно найти значение квантилей статистики для любого заданного уровня значимости. Квантиль порядка 0,95 равна 4,39, а квантиль порядка 0,99 — 8,75. Таким образом, гипотеза о равенстве средних по всем уровням (т. е. об отсутствии влияния фактора на переменную отклика) должна быть отвергнута, если уровень значимости α = 0,05, но не при уровне значимости α = 0,01. Таким образом, результаты дисперсионного анализа с достаточно вы­соким доверительным уровнем (> 95 %) указывают на наличие связи между численностью учащихся и числом возникновений инфекционных заболеваний в школах, т.е. качественно совпадают с результатами корреляционного анализа.

На рис. 4.27 приведен традиционный способ графического представления результатов дисперсионного анализа: средние по уровням фактора значения переменной отклика и показатели внутригруппового рассеяния (в данном случае приведены диапазоны изменений; могут быть использованы и другие показатели: стандартные отклонения средних, стандартные ошибки средних, доверительные интервалы для заданного уровня значимости). График показывает, что для некоторых уровней фактора риска показатели заболеваемости различаются существенно (соответствующие им интервалы изменения переменной отклика не пересекаются), но существуют и такие пары уровней, для которых внутригрупповой разброс гораздо больше разности между средними по уровням. Именно вследствие этого доверительный уровень для гипотезы о различии средних по уровням не достигает 99%.

Типичной для социально-гигиенического мониторинга является задача исследования влияния множественных факторов. В таких случаях для определения влияния каждого из них на переменную отклика недостаточно провести однофакторный дисперсионный анализ по каждому из факторов, поскольку для некоторых факторов их непосредственный эффект может быть мал по сравнению с эффектами его взаимодействия с другими факторами. В случае, если на переменную отклика оказывают влияние 2 независимых фактора А и В, разбиение общей суммы квадратов осуществляется с учетом взаимодействия факторов:

SSт = SS_А + SS_B + SS_АB + SS_R.

Не вдаваясь в подробности вычисления статистик, проверяющих гипотезу о равенстве всех средних по уровням для каждого включенного в модель фактора, отметим, что, как и в случае однофакторного анализа, все они строятся на соотношении с остаточной суммой квадратов и имеют F -распределение. Процедуры двухфакторного дисперсионного анализа имеются во всех статистических пакетах, а в некоторых пакетах есть и программы многофакторного дисперсионного анализа для случая более чем 2 факторов.

На рис. 4.28 приведены результаты анализа показателя заболеваемости, который регистрировали на 3 территориях ежемесячно в течении. 4 лет наблюдения, по фактору «год наблюдения» (таким образом, на каждый уровень этого фактора приходится по 36 наблюдений). Рисунок показывает, что, несмотря на тенденцию к росту среднего уровня заболеваемости со временем, различия средних для любой пары уровней недостоверны (в качестве показателя разброса взяты 95 %-е доверительные интервалы средних). Дисперсионный однофакторный анализ показал, что для данного фактора вероятность равенства всех средних по уровням равна 0,49.

Для фактора «территория» вероятность равенства всех средних по уровням оказалась меньше 0,0001, так как средние за период наблюдения уровни заболеваемости для разных территорий оказались резко различными (рис. 4.29).

При учете взаимодействия факторов «территория» и «год наблюдения» (т. е. неодинаковости динамики заболеваемости на разных территориях) в качестве отдельного фактора вероятность отсутствия влияния этого фактора на переменную отклика оказалась менее 0,0001. Та кой же уровень значимости имел место и для фактора «территория», а для фактора «год наблюдения» уровень значимости составил 0,0002. Более высокий уровень значимости для фактора «год наблюдения» по сравнению с комбинацией факторов «территория» и «год наблюдения» обусловлен тем, что выраженная динамика заболеваемости имела место только для одной из территорий, тогда как для двух других она оставалась стабильной (рис. 4.30). Таким образом, двухфакторный дисперсионный анализ с учетом взаимодействия факторов выявил как значимые различия средних уровней заболеваемости на различных территориях (выявляемые также и однофакторным анализом), так и наличие выраженной динамики заболеваемости (которая не выявляется однофакторным анализом, так как, во-первых, не имеет одинакового характера для всех территорий, а во-вторых, маскируется различиями средних уровней заболеваемости по территориям).

Статистика Фишера, используемая в дисперсионном анализе, основана на предположении о нормальности распределения переменной отклика на каждом уровне фактора. Дисперсионный анализ нечувствителен к небольшим отклонениям от нормального вида распределения, и поэтому может применяться, когда выборочные распределений не очень сильно отличаются от нормальных. Однако для существенно асимметричных распределений и в особенности при наличии наблюдений, резко отклоняющихся от средних, метод дисперсионного анализа неприемлем. В таких случаях следует пользоваться непараметрическим аналогом этого метода — ранговым критерием Крускала—Уомиса, проверяющим гипотезу о равенстве медиан для всех уровней фактора против альтернативы — существования пары уровней с неравными медианами (критерий реализован во всех статистических пакетах).

Задача 5. Пользуясь результатами примера 14, оцените достоверность влияния численности школьников на заболеваемость для диапазона изменений численности от 400 до 700. Квантили порядка (1 - α) для статистики F_3,4 равны 6,59 при α = 0,05 и 16,69 при α — 0,01.

Решение. Расчеты по схеме однофакторного дисперсионного анализа (см. табл. 4.7):

Таблица 4.7

i	j	yij	yi.	yij - yi.	(yij - yi.)2	yij - y..	(yij - y..)2	yi - y..	(yi. - y..)2
				-4		-1075	115,56	-6,75	45,56
						-2,75	7,56	-6,75	45,56
			18,5	-1,5	2,25	-6,75	45,56	-5,25	27,56
			18,5	1,5	2,25	-3,75	14,06	-5,25	27,56
				-2		0,25	0,06	2,25	5,06
						4,25	18,06	2,25	5,06
			33,5	-4,5	20,25	5,25	27,56	9,75	95,06
			33,5	4,5	20,25	14,25	203,06	9,75	95,06
Суммы							431,5		346,50

y.. = 190/8 = 23,75,

SS_T = 431,5, SS_в = 346,5, SS_R = 85,

I = 4, I-1=3, n — I = 4,

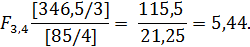
Полученное значение F-статистики немного ниже критического уровня (6.59), позволяющего отклонить гипотезу о равенстве всех средних по уровням с уровнем значимости а = 0,05. Таким образом, сокращение числа наблюдений привело к снижению достоверности вывода о зависимости заболеваемости в школах от численности школьников.