Анализ взаимосвязей между показателями внешней среды и здоровья представляет собой основную задачу социально-гигиенического мониторинга. Наиболее широкие возможности для такого анализа предоставляют количественные переменные. Если в непрерывных шкалах измеряются как фактор риска X, так и показатель здоровья Y, то взаимосвязь между ними может быть представлена в виде явной функиональной зависимости:
Y = f(X) + Ɛ,
где Ɛ — отклонение от однозначно определенной функции, связанное с влиянием других факторов и погрешностями наблюдения.
В терминах теории рисков такая зависимость называется зависимостью «доза—эффект». В статистике такое представление называется регрессионной зависимостью Y от X, или регрессией Y на X, а функция f — регрессионной функцией. Переменная X в этом случае называется независимой, а переменная Y — зависимой. Задачей регрессионного анализа является поиск функции f, максимально точно описывающей связь между этими переменными.
Если по экспериментальным данным удается с удовлетворительной степенью точности (т. е. с достаточно малой величиной отклонения) выразить зависимую переменную в виде явной функции от независимой, то полученная регрессионная зависимость может быть использована в целях прогнозирования значений зависимой переменной при таких уровнях фактора риска, для которых ее измерения не проводились. Точность такого прогноза зависит как от величины отклонения Ɛ (точности аппроксимации), так и от интервала, для которого построена регрессионная зависимость. В различных диапазонах изменения независимой переменной характер ее связи с зависимыми переменными может быть различным. Так, например, для многих факторов риска характерно наличие порога чувствительности и порога насыщения. Изменению уровня фактора риска в интервале между пороговыми значениями соответствуют выраженные изменения показателей здоровья, тогда как в области ниже порога чувствительности и выше порога насыщения (эти пороговые значения могут быть различными для разных показателей здоровья) такого влияния не наблюдается.
Простейшим видом функциональной зависимости является линейная зависимость:
Y = a + bX,
где a и b — коэффициенты (называемые регрессионными коэффициентами ими параметрами регрессии). График такой зависимости в координатной плоскости (X, Y) представляет собой прямую линию. В точке с координатами (0, а) эта прямая пересекает ось ординат (поскольку Y (0) = а), поэтому коэффициент а называется также точкой пересечения (intercept). Коэффициент b называется коэффициентом углового наклона (slоре). Его величина равна тангенсу угла между осью абсцисс и данной прямой.
Поиск зависимостей между факторами риска и показателями здоровья в линейном виде целесообразен не только по причине максимальной простоты такой зависимости, но еще и потому, что любую непрерывную зависимость в некотором диапазоне можно с достаточной степенью точности представить как линейную (при этом вид этой зависимости, т.е. значения коэффициентов регрессии, могут быть неодинаковыми для различных интервалов).
Мерой тесноты линейной связи между выборками служит выборочный коэффициент корреляции (или коэффициент корреляции Пирсона) r, определяемый по формуле
r = 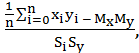
где n — объем выборок X и Y; xi, уi — i -ые значения этих выборок; Мx, Му — выборочные средние; SХ, Sу — выборочные стандартные уклонения.
В вычислениях удобно использовать другое (эквивалентное первому) выражение для коэффициента корреляции:
r = 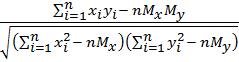 .
.
Можно показать, что коэффициент корреляции может принимать значения в диапазоне от -1 до +1. Знак коэффициента корреляции характеризует направленность связи между переменными X и Y. Положительный коэффициент корреляции соответствует ситуации, когда c ростом X увеличивается Y (положительная корреляционная связь), а отрицательный — убыванию Y с ростом X (отрицательная корреляционная связь). Абсолютная величина коэффициента корреляции характеризует степень тесноты линейной зависимости — чем ближе значение r к 1 или - 1, тем сильнее значения выборочных пар (xi, yi) сконцентрированы около регрессионной прямой (рис. 4.23, 4.24). Все значения выборочных пар (xi, yi) лежат на одной прямой тогда и только тогда, когда коэффициент корреляции между выборками X и Y равен ±1.
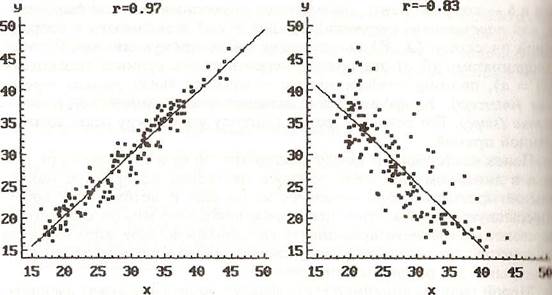
Рис. 4.23. Положительная корреляция Рис. 4.24. Отрицательная корреляции
между выборками между выборками
Для нормально распределенных случайных величин верно утверждение о том, что они некоррелированы в том и только в том случае, когда независимы. Поэтому близкое к 0 значение коэффициент корреляции между двумя выборками из нормальных генеральных совокупностей позволяет сделать вывод о независимости соответствующих переменных. Если же распределения исследуемых переменных не являются нормальными, некоррелированность выборок не дает достаточных оснований для вывода о независимости.
Коэффициенты а и b для прямой, для которой сумма расстояний от выборочных точек (xi, yi) минимальна, выражаются следующим образом:
a = My - bMx,
b = 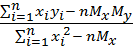 .
.
Можно показать, что линейное преобразование выборки, т. е. изменение масштаба и начала отсчета, не влияет на величину ее коэффициента корреляции с любой другой выборкой, если коэффициент изменения масштаба b положителен, и меняет знак коэффициента корреляции на противоположный при отрицательных значениях b.
Параметры линейной регрессии при таких преобразованиях изменяются: изменения начала отсчета приводят к изменению параметра а, и изменения масштаба — к изменению коэффициента наклона регрессионной прямой b.
Пример 12. В табл. 4.2 приведены данные о числе случаев возникновении инфекционных заболеваний в школах-интернатах за 5 лет в зависимости от численности учащихся.
Несмотря на то, что разброс показателя заболеваемости при одинаковых значениях численности достаточно велик (что свидетельствует о существовании других факторов, влияющих на заболеваемость), налицо факт увеличения числа заболеваний с ростом численности. Можно оценить интенсивность этой связи с помощью коэффициента корреляции, а также вычислить коэффициенты регрессии для зависимости заболеваемости от численности. Для упрощения расчетов воспользуемся свойством независимости коэффициента корреляции от преобразований масштаба переменных и выразим численность учащихся в сотнях. Исходные данные и необходимые для расчетов промежуточные значения приведены в табл. 4.3.
Мх = 54/12 = 4,5,
Му = 244/12 =20,33,
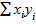 - nMxMy = 1 237 – 12 * 4,5 * 20,33 = 139,
- nMxMy = 1 237 – 12 * 4,5 * 20,33 = 139,
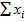 - nMx2 = 278 – 12 * 4,52 = 35,
- nMx2 = 278 – 12 * 4,52 = 35,
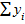 - nMy2 = 5690– 12 * 20,332 = 728,67,
- nMy2 = 5690– 12 * 20,332 = 728,67,
r = 139/ 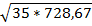 = 0,87;
= 0,87;
b = 139/35 = 3,97 (если численность выражать не в сотнях, а в единицах, то этот коэффициент следует уменьшить в 100 раз, т.е. b = 0,0397); а = 20,33 - 3,97 * 4,5 = 2,46.
Полученное значение коэффициента корреляции достаточно близко к 1. Это свидетельствует о том, что между численностью школьников в интернате и частотой возникновения инфекционных заболеваний существует положительная корреляционная связь.
Если для каждого значения независимой переменной хі, вычислить соответствующее ему регрессионное значение
yi регр . = a + bxi,
то можно показать, что для построенной таким образом выборки регрессионных значений Y регр. сумма квадратов отклонений от ее среднего значения не превосходит суммы квадратов отклонений для выборки Y, а квадрат коэффициента корреляции равен отношению квадратов отклонений выборок Y регр. и Y. Поэтому квадрат коэффициента корреляции служит мерой точности линейной аппроксимации зависимой переменной. Сумму квадратов отклонений выборки регрессионных значений называют объясняемой, или модельной, составляющей рассеяния выборки Y, поскольку она объясняет рассеяние зависимой переменной, обусловленное ее связью с независимой переменной. Разность между суммами квадратов выборок Y и Y регр. называют остаточным рассеянием. Квадрат коэффициента корреляции показывает, какую долю рассеяния зависимой переменной можно объяснить влиянием независимой переменной. В рассмотренном примере r2 = 0,76, т. е. более 3/4 рассеяния заболеваемости можно отнести к эффекту численности.
Чем меньше число наблюдений, тем ниже точность оценки любых выборочных характеристик, в том числе и коэффициента корреляции, поэтому высокое значение коэффициента корреляции не обязательно означает наличие достоверной связи между переменными. Для нормального распределенных переменных существует статистический критерий, позволяющий оценить вероятность отличия их коэффициента корреляции от 0. Во всех современных статистических пакетах процедуры корреляционного анализа обеспечивают выдачу уровней значимости для гипотезы о равенстве 0 выборочного коэффициента корреляции, а процедуры регрессионного анализа — вычисление стандартных ошибок регрессионных коэффициентов и вероятностей равенства этих коэффициентов 0. Для рассмотренного выше примера Р(r = 0) = 0,002, а значения параметров регрессии с учетом ошибки равны: а = 2,46 ± 3,42; b = 3,97 ± 0,71; Р(а = 0) = 0,49; Р(b = 0) < 0,001 (вычисления выполнены с помощью пакета Statgraphics). Следовательно, несмотря на высокое значение коэффициента корреляции и достоверно отличный от 0 коэффициент наклона регрессионной прямой, регрессионная зависимость не является надежной. Такой результат связан с тем, что зависимость между численностью и заболеваемостью не вполне линейна (рис. 4.25) и лучше аппроксимируется экспоненциальной функцией (рис. 4.26).
Процедура экспоненциальной регрессии, т. е. поиск параметров зависимости в виде
Y = 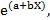
реализованная во всех статистических пакетах, сводится к задаче линейной регрессии логарифмированием переменной Y:
ln Y = а + bХ.
Таблица 4.2
| Численность учащихся и число инфекционных заболеваний за 5 лет |
в школах-интернатах
| Номер школы | Число учащихся (округление до сотен) | Число случаев инфекционных заболеваний |
Таблица 4.3
Расчет выборочного коэффициента корреляции Пирсона
| i | xi | yi | xi yi | xi2 | yi2 |
| Суммы |
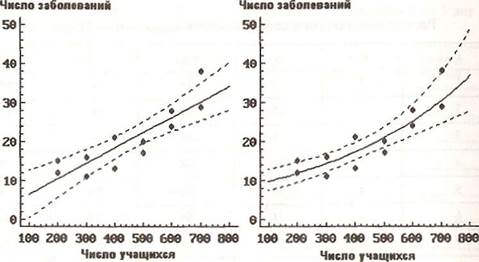
Рис. 4.25. Линейная регрессия и 95 %-е Рис. 4.26. Экспоненциальная регрессия
доверительные интервалы регрессии и 95 %-е доверительные интервалы рег-
рессии
Очевидно, что такое преобразование допустимо, только если в выборке Y содержатся только положительные значения, и что удовлетворяющие такой зависимости переменные X и Y не могут одновременно иметь нормальное распределение. Наилучшие результаты экспоненциальная регрессия дает в случае, если переменная X распределена по нормальному закону, а Y — по логнормальному (в этом случае корректны вычисления ошибок параметров регрессии и доверительных интервалов для регрессионных значений). Для рассмотренного примера экспоненциальная регрессия дает следующие результаты:
а = 2,09 ± 0,16,
Р(а=0) ˂ 0,0001,
b = 0,0019 ± 0,003,
Р(b=0) ˂ 0,0003,
r = 0,88, r2 = 0,78.
По сравнению с линейной регрессией увеличилась и доля объясняемого рассеяния, и достоверность полученных оценок.
При решении задач социально-гигиенического мониторинга нередки случаи, когда невозможно с удовлетворительной степенью точности выразить исследуемый показатель здоровья через единственный показатель внешней среды. В этом случае необходимо использовать методы множественной регрессии, т. е. искать выражение показателя здоровья Y в виде
Y = f(X1, X2, …, Xn) + Ɛ,
где X1, X2, …, Xn — различные показатели среды. Простейшим видом такой зависимости является линейная зависимость вида:
Y = a +b1X1 + b2X2 + … + bnXn.
Для того чтобы коэффициенты этой зависимости можно было определить однозначно, необходимо, чтобы факторы были взаимно независимы (если все они распределены по нормальному закону, для этого достаточно, чтобы они были некоррелированы). Процедуры множественной линейной регрессии содержатся во всех статистических пикетах.
Если распределения исследуемых величин отличаются от нормального, для оценки тесноты связи между ними используются непараметрические методы: ранговый коэффициент корреляции Спирмена и ранговый коэффициент корреляции Кендалла. Оба метода работают не с численными значениями переменных, а с их рангами. Первый из этих методов используется для непрерывных случайных величин, распределения которых сильно отличаются от нормального, а второй — для случайных величин, измеряемых в балльных шкалах с большим числом градаций, но не обязательно равноценными интервалами между соседними градациями, т.е. для переменных, более близких к ординальным, чем к чисто количественным.
Ранговый коэффициент корреляции Спирмена основан на независимом ранжировании обеих исследуемых выборок. Каждому значению в этих выборках присваивается ранг (rk), т.е. порядковый номер этого значения (по возрастанию). Если в выборке имеются равные значения, используется модифицированная формула для расчета коэффициента корреляции Спирмена. Вместо использования этой модификации, существенно усложняющей расчеты, можно присваивать равным значениям одинаковые ранги, равные среднему арифметическому соответствующих номеров. Ранги в таком случае могут принимать дробные значения, а точность вычисления коэффициента ранговой корреляции практически не страдает. Для каждого значения индекса і рассчитывается величина di, равная разности рангов xi и yi. Формула для рангового коэффициента корреляции Спирмена R имеет следующий вид:
R = 1 - 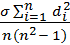
Пример 13. Для данных из примера 12 ранговый коэффициент корреляции Спирмена рассчитывается следующим образом (см. табл. 4.4):
R = 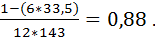
Значение рангового коэффициента корреляции Спирмена оказалось несколько выше коэффициента корреляции Пирсона и совпало с коэффициентом корреляции между логарифмом численности и заболеваемостью. Вообще оценка корреляции по Спирмену дает более высокие результаты, чем обычный коэффициент корреляции в случае, когда связь между переменными монотонна, но при этом нелинейна.
Задача 4. Для 5 населенных пунктов интегральная оценка загрязнения окружающей среды составила 2, 3, 4, 5 и 7 баллов, а состояние здоровья населения — соответственно, 7, 6, 4, 5 и 3 балла (оба показателя измеряли по 10-балльным шкалам). Вычислить коэффициенты корреляции Пирсона и Спирмена между показателями загрязнения и состояния здоровья.
Решение. Вспомогательные величины для расчетов приведены в табл. 4.5.
Таблица 4.4
Расчет рангового коэффициента корреляции Спирмена
| i | xi | yi | rk (xi) | rk (yi) | di | di2 | |
| 1,3 | -0,5 | 0,25 | |||||
| 1,5 | -2,5 | 6,25 | |||||
| 3,5 | 2,5 | 6,25 | |||||
| 3,5 | -1,5 | 2,25 | |||||
| 5,5 | 2,5 | 6,25 | |||||
| 5,5 | -2,5 | 6,25 | |||||
| 7,5 | 1.5 | 2,25 | |||||
| 7,5 | 0,5 | 0,25 | |||||
| 9,5 | 0,5 | 0,25 | |||||
| 9,5 | -0,5 | 0,25 | |||||
| 11,5 | 0,5 | 0,25 | |||||
| 11,5 | -0,5 | 0,25 | |||||
| Сумма | 33,5 |
Таблица 4.5
| i | xi | yi | xi yi | xi2 | yi2 | rk (xi) | rk (yi) | di | di2 |
| -4 | |||||||||
| -2 | |||||||||
| Суммы |
Расчет выборочного коэффициента корреляции Пирсона:
Мх = 21,5 = 4,2,
Му = 25/5,
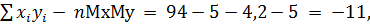
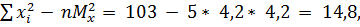
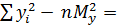 135-5*5*5 = 10,
135-5*5*5 = 10,
r = 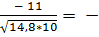 0,904.
0,904.
Расчет рангового коэффициента корреляции Спирмена:
R = 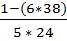 = -0,9.
= -0,9.
 2015-07-14
2015-07-14 2234
2234
