Методы сравнения выборок

Эта группа методов используется для анализа количественных показателей здоровья в двух ситуациях: если фактор риска имеет всего 2 уровня (например, в задачах сравнения показателей здоровья в группах людей, подверженных и не подверженных воздействию некоторого фактора), а также если фактор риска имеет несколько градаций, причем дисперсионный анализ отклонил гипотезу о равенстве средних переменной отклика по всем уровням фактора, и требуется уточнить, каким именно уровням фактора риска соответствуют различные уровни переменной отклика. Выбор конкретного метода сравнения выборок определяется двумя обстоятельствами: являются ли эти выборки попарно связанными или независимыми и соответствуют ли их распределении нормальному закону.

В случае нормальности выборок для их сравнения используется параметрический критерий Стьюдента (t -критерий) — одновыборочный для попарно связанных выборок и двухвыборочный для независимых. Этот критерий основан на сравнении выборочных средних.

Одновыборочный t -критерий предназначен для проверки нулевой гипотезы о равенстве среднего М_х нормально распределенной выборки X заданному числу М₀ против двухсторонней альтернативы М_х ≠ М₀ или односторонней альтернативы М_х ˂ М₀ (или М_х > М₀). Если выборка X имеет объем n и стандартное отклонение S и нулевая гипотеза верна, то статистика

t =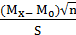

имеет t-распределение с (n — 1) степенью свободы. Область принятия нулевой гипотезы с заданным уровнем значимости α для двухсторонней альтернативы соответствует интервалу между квантилями t-распределения с (п - 1) степенью свободы порядка α/2 и (1 — α/2), для односторонней альтернативы М_х < Мо — области от -∞ до квантили порядка (1 — α), а для односторонней альтернативы М_х > Мо — области от квантили порядка α до +∞. Следует иметь в виду, что в силу симметричности t -распределения относительно оси ординат квантиль порядка α/2 равна квантили порядка (1 - α/2), взятой со знаком «минус».

Если попарно связанные выборки X и Y распределены нормально, то выборка (X — Y) также имеет нормальное распределение, поэтому проверка гипотезы о равенстве средних выборок X и Y эквивалентна проверке гипотезы о равенстве 0 среднего их разности М_d, которая и выполняется с помощью одновыборочного t -критерия.

Пример 16. Среднегодовые уровни заболеваемости (на 1 000 населения) и 6 районах одной области составили в 1990 г. 800, 826, 894, 910, 924 и 1 106, а в 1995 г. — соответственно, 1 229, 1 045, 1 294, 1 496, 1 311 и 1 101. Схема расчетов одновыборочной t -статистики для проверки гипотезы о равенстве средних попарно связанных выборок приведена в табл. 4.10.

Таблица 4.10

Расчет статистики одновыборочного t -критерия

i	xi	yi	di = xi - yi	di2
			-429
			-219
			-400
			-586
			-387
		1 101
Сумма			-2 016
Среднее			-336

S_d² = 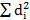– n ( М_d )² = 885 192 – 6 * (-336)² = 207 816,

t =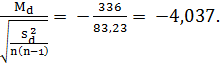

Для 5 степеней свободы табличное значение 0,995-й квантили t -распределения равно 4,032, следовательно гипотеза о постоянстве среднего уровня заболеваемости должна быть отвергнута с уровнем значимости α = 0,01, а гипотеза о том, что заболеваемость увеличилась, может быть принята с доверительным уровнем 99,5 %.

Если выборки X и Y — независимые выборки из нормально распределенных генеральных совокупностей с объемами п_х, п_у, средними М_х, М_у, стандартными отклонениями S_x, S_y и суммами квадратов отклонений от средних SS_х, SS_у, то статистика t -критерия, проверяюшего нулевую гипотезу о равенстве средних М_х = М_у против двухсторонней или односторонней альтернативы, имеет t -распределение с (n _х + n _у — 2) степенями свободы и определяется по формуле:

t =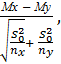

где объединенная дисперсия двух выборок 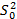определяется из соотношений:

= = .

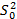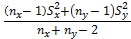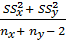Множество принятия нулевой гипотезы при заданном уровне значимости в зависимости от альтернативы определяется так же, как и в случае одновыборочного критерия.

Следует иметь в виду, что такой вариант t -критерия применим только в случае, если дисперсии выборок одинаковы. Если же дисперсии выборок существенно различаются, то в качестве статистики критерия используется величина:

t =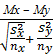

(так называемая разделенная t -статистика). Число степеней свободы t -статистики также определяется иначе, чем для случая равных дисперсий. Поэтому в некоторых статистических пакетах, в частности в пакете Statgraphics, процедура двухвыборочного t -критерия включает также проверку гипотезы о равенстве выборочных дисперсий, вычисление значения разделенной t -статистики и соответствующего ей числа степеней свободы.

Пример 17. Сравним выборку данных по заболеваемости за 1990 г. из примера 16 с данными, полученными в том же году для 5 районов другой области и равными 630, 700, 706, 824 и 872. Схема расчета двухвыборочной t -статистики приведена в табл. 4.11.

М_х- М_у = 163,6,

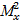= 828 100,

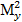= 557 112,96,

SS_x = 5 026 624 - 6 ∙ 910² = 58 024,

SS_у = 2 824 696 - 5 ∙ 746,4² = 39 131,2,

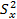= 58 024/5 = 11064,8

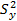=39131,2/4= 9 782,8

Дисперсии выборок приблизительно совпадают, поэтому можно пользоваться объединенной t -статистикой:

SS_x + SS_у = 97 155,2,

t =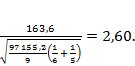

Для t -статистики с 9 степенями свободы 90 %-я точка распределения раина 1,83, а 95%-я — 2,26. Таким образом, при 95% доверительном уровне может быть принята как односторонняя альтернативная гипотеза о том, что среднее первой выборки превышает среднее второй, так и двухсторонняя альтернатива.

Если выборочные распределения отличаются от нормальных, для (равнения выборок используются непараметрические критерии. Для попарно связанных выборок в качестве непараметрических аналогов одновыборочного критерия Стьюдента наиболее широко используются критерий знаков и критерий знаковых рангов Виякоксона.

Критерий знаков предельно прост: каждой паре значений (x_i, у_i) ставится в соответствие знак +, если x_i,˃ у_i, и -, если x_i, <, у_i. Если x_i = у_i, то такая пара исключается из рассмотрения и объем выборок уменьшается на 1. Нулевая гипотеза о том, что между выборками не наблюдается сдвига, отвергается в том случае, если один из знаков встречается существенно чаще, чем другой. Статистикой критерия знаков является число появлений преобладающего знака. Поскольку при сравнении значений пар (x_i, у_i) не используются абсолютные значения, а используется лишь отношение порядка «больше/меньше» или

Таблица 4.11

Расчет статистики двухвыборочного t-критерия

i	xi	yi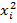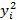
			640 000	396 900
			682 276	490 000
			799 236	498 436
			828 100	678 976
			853 776	760 384
	1 106	-	1 223 236	-
Сумма			5 026 624	2 824 696
Среднее		746,4

«лучше/хуже», критерий знаков может использоваться для сравнении переменных, измеряемых в порядковых шкалах.

Критерий знаковых рангов Вилкоксона учитывает не только знак, но и величину разностей. Абсолютные величины разностей ранжируются по возрастанию, после чего подсчитывается средний ранг отделит для положительных и для отрицательных разностей. Гипотеза об отсутствии сдвига между выборками отвергается, если эти средние ранги существенно различаются.

Пример 18. Используем непараметрические критерии для сравнения по парно связанных выборок из примера 16. Все значения, необходимые дли расчетов статистик критерия знаков и Вилкоксона, приведены в табл. 4.12.

Таблица 4.12

Сравнение попарно связанных выборок с помощью непараметрических критериев

i	xi	yi	di = xi – yi	Ранг | di |
			-429
			-219
			-400
			-586
			-387
б

Статистика критерия знаков равна 5. В таблицах распределения этой статистики для n = 6 минимальное число одинаковых знаков, позволяющее принять гипотезу о различии выборок с доверительным уровнем не ниже 95 %, равно 6. Таким образом, критерий знаков не позволяет считать рост заболеваемости достоверным. Такой доверительный уровень при наличии единственной разности, противоположной всем остальным, достигается только при n ≥9.

Критерий Вилкоксона для случая, когда положительная разность одна и ранг ее равен 1, а отрицательных разностей пять со средним рангом (2 + 3 + 4 + 5 + 6)/5 = 4, дает оценку вероятности отсутствия сдвига между выборками, равную 0,059, т. е. близкую к 5 %-му уровню значимости, но все же превышающую этот уровень. Таким образом, непараметрические критерии по сравнению с критерием Стьюдента оценивают различия между уровнями заболеваемости в 1990 и 1995 гг. как менее значимые.

Наиболее популярным непараметрическим критерием для сравнения независимых выборок является критерий Манна—Уитни, основанный на ранжировании выборки, полученной объединением исходных. Для обеих выборок подчитывается их средний ранг, и гипотеза о различии выборок принимается в случае, если их средние ранги существенно различаются.

Все перечисленные методы сравнения выборок реализованы во всех специализированных статистических пакетах.

Рекомендуемая литература

1. Бредфорд Хилл А. Основы медицинской статистики. М.: Медгиз, 1958. 306 с.

2. Боровиков В. П. Популярное введение в программу SТАТISTIСА. М.: Ком­пьютер Пресс, 1998. 267 с.

3. Дюк В. Обработка данных на ПК в примерах. СПб.: Питер, 1997. 240с.Компьютерная биометрика / Под ред. В. Н. Носова. М.: Изд-во МГУ, 1990. 232с

4. Тюрин Ю. Н., Макаров А. А. / Под ред. В. Э. Фигурнова. Статистический анализ данных на компьютере. М.: ИНФРА-М, 1998. 528с.