8.1. Определение производной функции в точке.
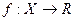
 - внутренняя точка из области определения, т.е. она лежит в области определения вместе с некоторой своей окрестностью (
- внутренняя точка из области определения, т.е. она лежит в области определения вместе с некоторой своей окрестностью (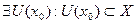 ).
).
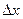 - приращение переменной.
- приращение переменной.
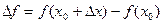
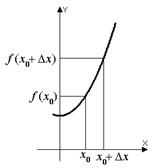
Производной функции в точке  называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.
называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.
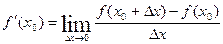
Если предел существует и конечен, то функция называется дифференцируемой в точке  .
.
Пример 1:
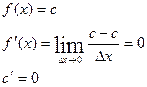
Пример 2:
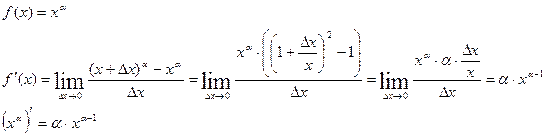
Пример 3:
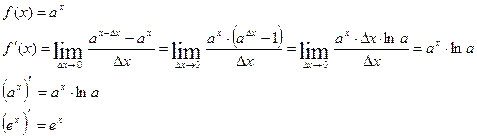
Пример 4:
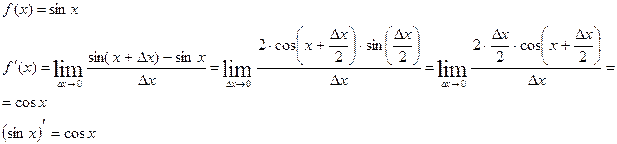
Пример 5:
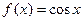
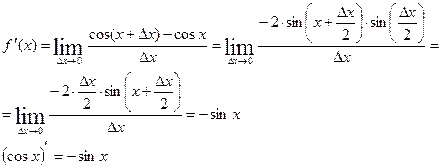
8.2. Односторонние производные. Связь непрерывности функции в точке с существованием конечной производной.
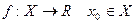
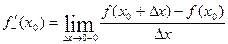 - производная слева функции
- производная слева функции 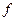 в точке
в точке  .
.
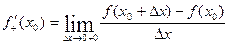 - производная справа функции
- производная справа функции 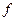 в точке
в точке  .
.
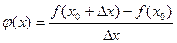
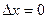 не лежит в области определения.
не лежит в области определения.
По теореме о связи существования конечного предела с односторонним пределом:
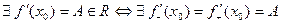 .
.
Т. О связи непрерывности функции в точке с существованием конечной производной.
Если функция имеет конечную производную в точке, то она непрерывна в этой точке.
Доказательство:
По условию 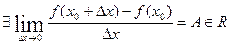

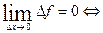 (по определению)
(по определению) 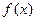 непрерывна в точке
непрерывна в точке  , ч.т.д.
, ч.т.д.
Обратное не верно.
Пример 1: 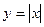 в точке
в точке  непрерывна, т.к.
непрерывна, т.к.
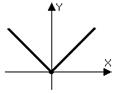
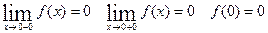
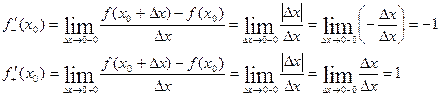
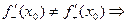 не существует производной.
не существует производной.
Пример 2:
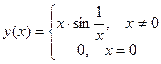
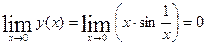 (т.к.
(т.к. 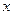 - б.м.,
- б.м., 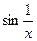 - ограниченная)
- ограниченная)
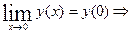
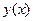 непрерывна в точке
непрерывна в точке 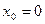
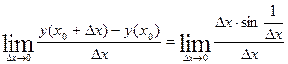 не существует.
не существует.
8.3. Правила вычисления производной. Таблица производных.
(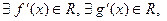 )
)
1) 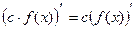
2) 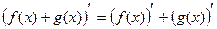
3) 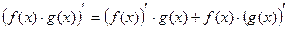
Доказательство:
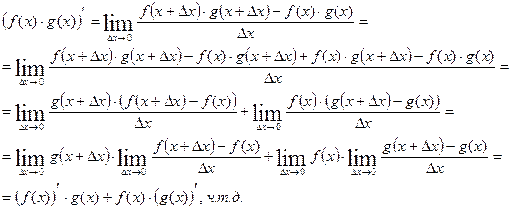
4) 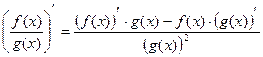
Доказательство:
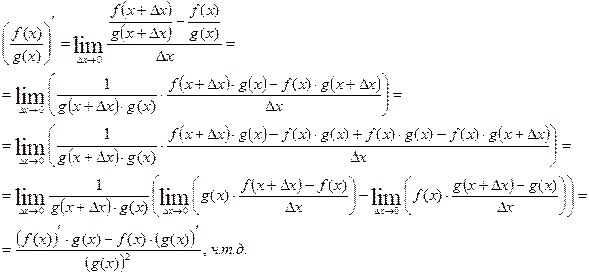
5) 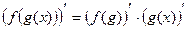
Доказательство:
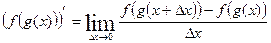
Обозначим 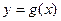 .
.
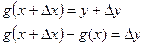
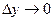 при
при 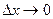 в силу непрерывности
в силу непрерывности 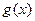 .
.
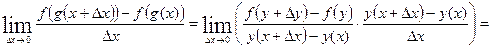
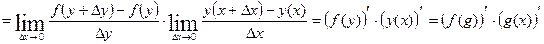 , ч.т.д.
, ч.т.д.
6) 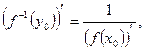 где
где 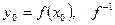 непрерывна в точке
непрерывна в точке 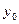 .
.
Доказательство:
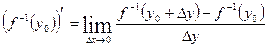
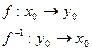
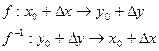
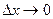 при
при 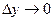 , т.к.
, т.к. 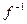 непрерывна.
непрерывна.
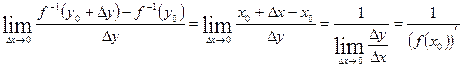 , ч.т.д.
, ч.т.д.
7) 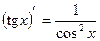
Доказательство:
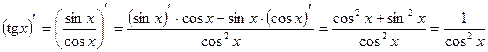 , ч.т.д.
, ч.т.д.
8) 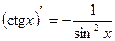
Доказательство:
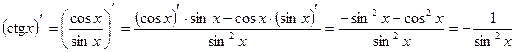 , ч.т.д.
, ч.т.д.
9) 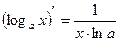
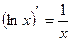
Доказательство:
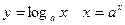
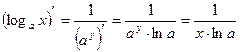 , ч.т.д.
, ч.т.д.
10) 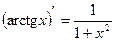
Доказательство:
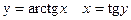
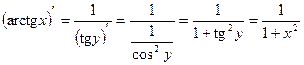 , ч.т.д.
, ч.т.д.
11) 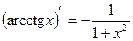
Доказательство:
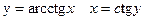
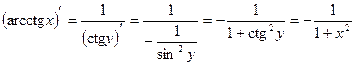 , ч.т.д.
, ч.т.д.
12) 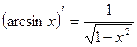
Доказательство:
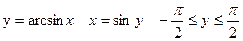
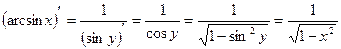 , ч.т.д.
, ч.т.д.
13) 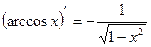
Доказательство:
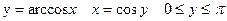
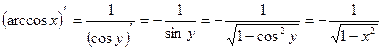 , ч.т.д.
, ч.т.д.
14) 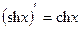
Доказательство:
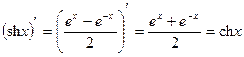 , ч.т.д.
, ч.т.д.
15) 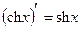
Доказательство:
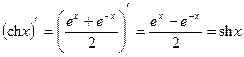 , ч.т.д.
, ч.т.д.
16) 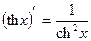
Доказательство:
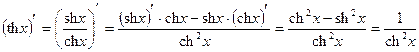 , ч.т.д.
, ч.т.д.
17) 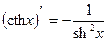
Доказательство:
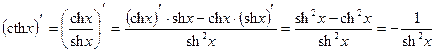 , ч.т.д.
, ч.т.д.
Таблица производных
1) 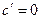
2) 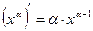
3) 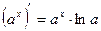
4) 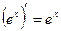
5) 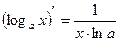
6) 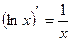
7) 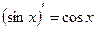
8) 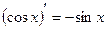
9) 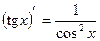
10) 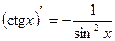
11) 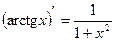
12) 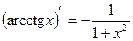
13) 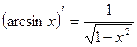
14) 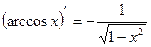
15) 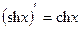
16) 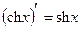
17) 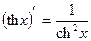
18) 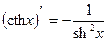
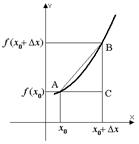
8.4. Физический и геометрический смысл производной.
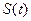 - путь, пройденный к моменту
- путь, пройденный к моменту 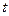 .
.
Зафиксируем 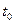 .
.
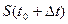 - путь, пройденный к моменту
- путь, пройденный к моменту 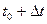 .
.
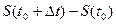 - путь, пройденный за время
- путь, пройденный за время 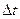 .
.
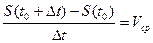 (средняя скорость)
(средняя скорость)
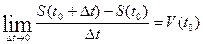 (мгновенная скорость)
(мгновенная скорость)
Физический смысл производной: 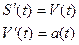 .
.
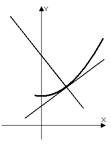
Геометрический смысл:
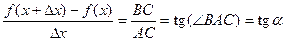 (угол наклона секущей AB).
(угол наклона секущей AB).
Если  , то т. B
, то т. B  т. A и секущая становится касательной.
т. A и секущая становится касательной.
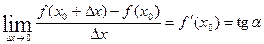
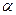 - угол наклона к оси
- угол наклона к оси 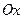 касательной к графику функции
касательной к графику функции 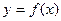 в точке
в точке  .
.
Уравнение касательной и нормали.
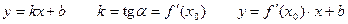
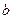 найдем из условия, что точка
найдем из условия, что точка 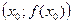 лежит на прямой.
лежит на прямой.
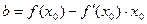
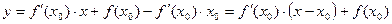
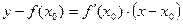 - уравнение касательной в точке
- уравнение касательной в точке 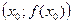 .
.
Нормаль – прямая, проходящая через точку 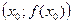 и перпендикулярная касательной.
и перпендикулярная касательной.
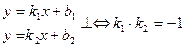
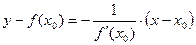 - уравнение нормали в точке
- уравнение нормали в точке 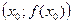 .
.
8.5. Степенно-показательная функция. Логарифмическое дифференцирование.
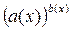 - степенно-показательная функция.
- степенно-показательная функция.
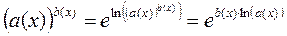
Если точка  такая, что
такая, что 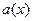 и
и 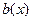 непрерывны в этой точке и
непрерывны в этой точке и 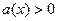 , тогда
, тогда 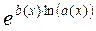 тоже непрерывна в точке
тоже непрерывна в точке  (по теореме о непрерывности композиции и произведения непрерывных функций).
(по теореме о непрерывности композиции и произведения непрерывных функций).
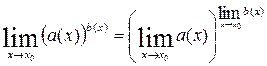 .
.
Вычисление производной:
1)
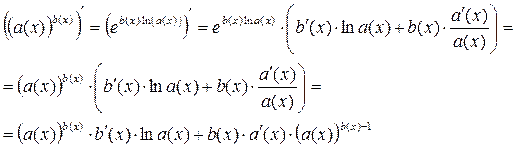
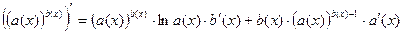
2) 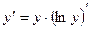 - уравнение для логарифмического дифференцирования.
- уравнение для логарифмического дифференцирования.
Пример: 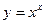
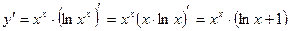
Логарифмическое дифференцирование употребляется не только при дифференцировании степенно-показательных функций, но и когда это упрощает вычисления.
8.6. Дифференцируемость функции в точке. Дифференциал.
Функция дифференцируема в точке, если ее приращение представимо в виде суммы главной линейной части относительно приращения переменной (дифференциала) и бесконечно малой более высокого порядка, чем приращение переменной.
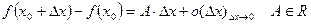
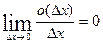 .
.
Пример: 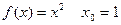
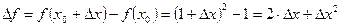
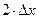 - главная линейная часть (дифференциал).
- главная линейная часть (дифференциал).
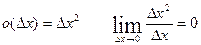
Т. Необходимое и достаточное условие дифференцируемости.
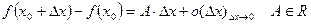 (функция дифференцируема в точке
(функция дифференцируема в точке  )
) 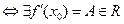 .
.
Доказательство:
(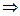 ) (необходимость)
) (необходимость)
Пусть 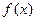 дифференцируема в точке
дифференцируема в точке 
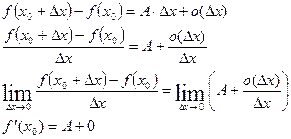
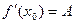 , ч.т.д.
, ч.т.д.
( ) (достаточность)
) (достаточность)
Пусть 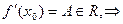
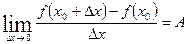
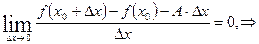
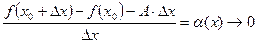 - б.м. при
- б.м. при 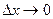 .
.
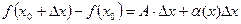 , где
, где 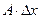 - главная линейная часть (дифференциал),
- главная линейная часть (дифференциал), 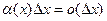 , ч.т.д.
, ч.т.д.
Пример: 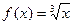 не дифференцируема в точке
не дифференцируема в точке 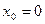 .
.
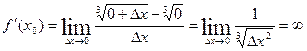 - не существует конечной производной, значит функция не дифференцируема.
- не существует конечной производной, значит функция не дифференцируема.
Если производная в точке равна 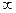 , то в этой точке вертикальная касательная.
, то в этой точке вертикальная касательная.
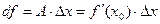
Если 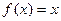 , то
, то 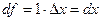
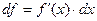
Привала для вычисления дифференциала.
1) 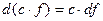
2) 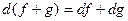
3) 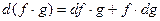
4) 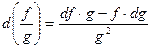
Доказательство:
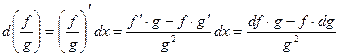 , ч.т.д.
, ч.т.д.
5) Инвариантность дифференциала
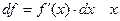 - независимая переменная.
- независимая переменная.
Пусть 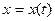 .
. 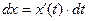 , тогда
, тогда 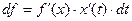 . Т.к.
. Т.к. 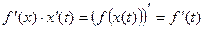 , то
, то 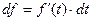 .
.
Инвариантность дифференциала заключается в том, что дифференциал всегда имеет один и тот же вид: произведение производной по некоторой переменной на приращение этой переменной - не зависимо от того, будет ли эта переменная независимой, либо сама будет функцией от некоторой переменной.
Геометрический смысл дифференциала.
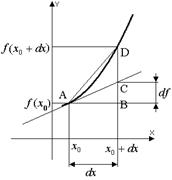
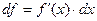
Геометрический смысл 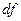 состоит в том, что он равен приращению, которое получает касательная к графику
состоит в том, что он равен приращению, которое получает касательная к графику 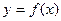 в точке
в точке  при переходе от точки
при переходе от точки  к точке
к точке 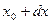 .
.
Приближенные вычисления с помощью дифференциала.
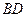 - приращение функции (
- приращение функции (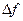 ).
).
При малых 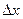
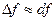 .
.
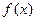 дифференцируема в точке
дифференцируема в точке  , т.е.
, т.е.
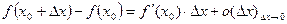
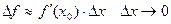
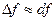
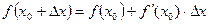 - уравнение для приближенных вычислений значений функций.
- уравнение для приближенных вычислений значений функций.
Пример 1: 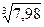
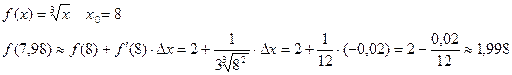
Пример 2: 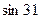 º
º 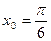
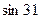 º=
º= 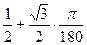
8.7. Производные высших порядков.
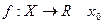 - внутренняя точка области определения.
- внутренняя точка области определения.
Пусть в некоторой 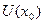 везде существует производная:
везде существует производная: 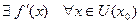 .
.
Т.о. 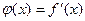 определена в окрестности
определена в окрестности 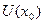 ,
, 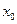 - внутренняя точка области определения для
- внутренняя точка области определения для 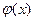 .
.
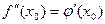
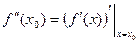
Аналогично определяется производная третьего порядка и т.д.
Пример 1: 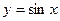
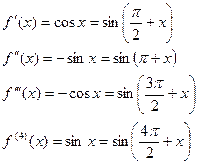
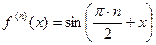
Пример 2: 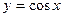
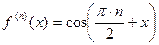
Правила для вычисления 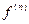 .
.
1) 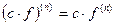
2) 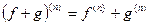
3) 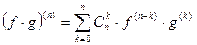 - формула Лейбница
- формула Лейбница
Доказательство: (ММИ)
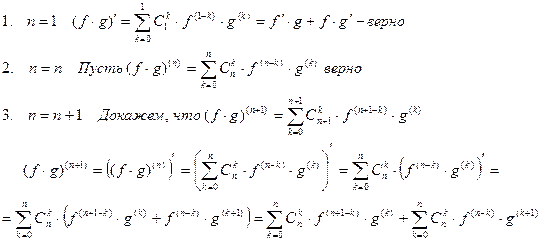
Обозначим 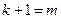 ,
,
тогда второе слагаемое примет вид 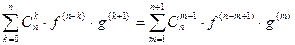 .
.
Заменим m на k. 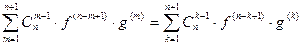 .
.
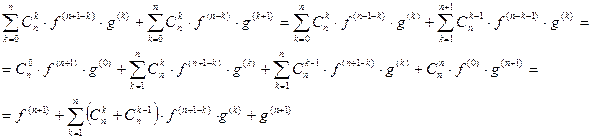
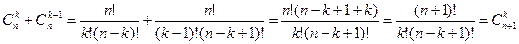
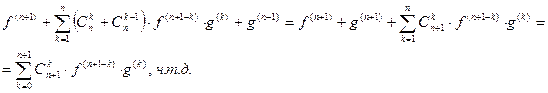
Пример: 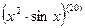
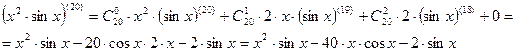
8.8. Функции, заданные параметрически. Производная функции, заданной параметрически.
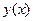 задана параметрически:
задана параметрически: 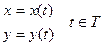 .
.
Физический смысл:
Это можно понимать как координаты точки на плоскости в момент времени 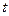 .
.
Иногда параметр можно выразить из системы и представить функцию в явном виде.
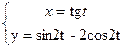
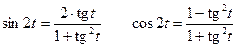
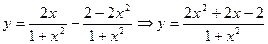 - функция задана явно.
- функция задана явно.
Как считать производную функции, заданной параметрически, если нельзя выразить функцию явно?
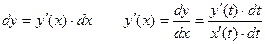
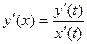
Пример 1:
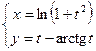
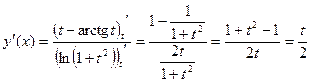
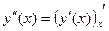
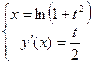
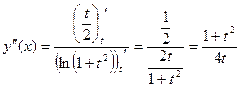
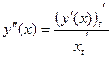
Пример 2: Написать уравнение касательной к функции 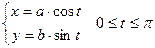 в точке
в точке 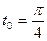 .
.
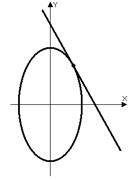
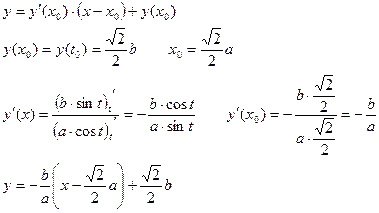
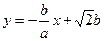 - уравнение касательной в точке
- уравнение касательной в точке 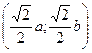 .
.
8.9. Производная функции, заданной неявно.
Неявное задание – один из способов задания функции.
 - уравнение задает функцию
- уравнение задает функцию 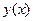 .
.
Пример: 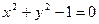
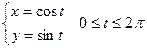
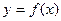 - функция задана явно
- функция задана явно
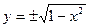
Как считать производную функции, заданной неявно?
Нужно равенство 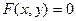 дифференцировать как тождество, считая
дифференцировать как тождество, считая 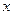 независимой переменной, а
независимой переменной, а 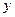 - функцией от
- функцией от 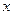 .
.
Пример 1: 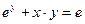
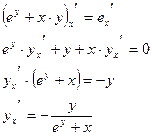
Пример 2:
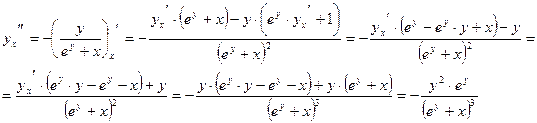
Можно упрощать, используя первоначальное уравнение 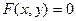 .
.
8.10. Дифференциалы высшего порядка.
Дифференциал второго порядка – это дифференциал от дифференциала первого порядка.
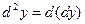
Дифференциал первого порядка – это функция от двух переменных: 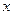 и приращения
и приращения 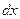 .
.
Зафиксируем 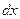 :
:
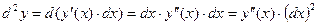
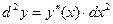 (1)
(1)
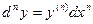
Свойства дифференциала 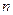 -того прядка.
-того прядка.
1) 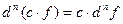
2) 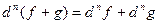
3) 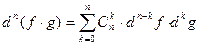
4) Свойство инвариантности, справедливое для дифференциала первого порядка, для дифференциала  -того прядка не верно.
-того прядка не верно.
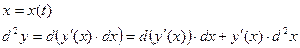
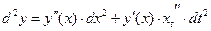 (2)
(2)
Формулы (1) и (2) отличаются вторым слагаемым. Если оно не равно нулю, то свойство инвариантности не выполняется.
Если 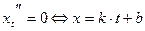 , то свойство инвариантности выполняется.
, то свойство инвариантности выполняется.
8.11. Основные теоремы дифференциального исчисления.
Т.1. Теорема Ферма.
Пусть:1) функция определена на промежутке
2)  - внутренняя точка промежутка
- внутренняя точка промежутка
3) функция в точке  принимает наибольшее значение, т.е.
принимает наибольшее значение, т.е. 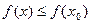 для всех других точек
для всех других точек
4) существует конечная производная в точке  .
.
Тогда 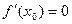 .
.
Доказательство:
По условию 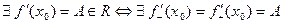 .
.
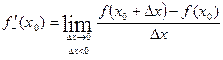
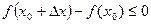 (по условию), значит
(по условию), значит 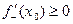
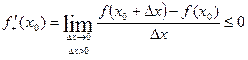 , значит
, значит
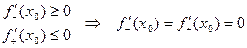 , ч.т.д.
, ч.т.д.
Геометрический смысл теоремы Ферма: если в точке, в которой функция принимает наибольшее (наименьшее) значение, существует касательная, то она параллельна оси  .
.
Т.2. Теорема Роля.
Пусть:1) 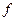 определена и непрерывна на отрезке
определена и непрерывна на отрезке 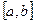
2) 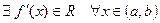
3) 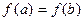 .
.
Тогда внутри отрезка найдется точка, в которой производная функции обращается в нуль, т.е. 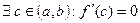
Доказательство:
Пусть 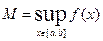
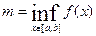
I сл) 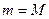 , тогда
, тогда 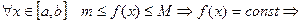
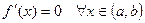
II сл) 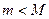 . Поскольку функция на концах отрезка принимает одинаковые значения, то одно из значений (либо
. Поскольку функция на концах отрезка принимает одинаковые значения, то одно из значений (либо 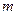 , либо
, либо 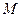 ) достигается во внутренней точке
) достигается во внутренней точке 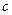 . Тогда для точки
. Тогда для точки 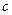 выполняются все условия теоремы Ферма, значит
выполняются все условия теоремы Ферма, значит 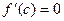 , ч.т.д.
, ч.т.д.
Геометрический смысл теоремы Роля: если функция удовлетворяет условиям теоремы Роля, тогда найдется точка, в которой касательная параллельна оси 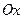 .
.
Т.3. Теорема Лагранжа.
Пусть:1) 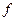 определена и непрерывна на отрезке
определена и непрерывна на отрезке 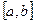
2) 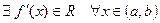
Тогда найдется точка внутри отрезка такая, что производная в этой точке будет равна 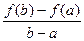 , т.е.
, т.е. 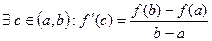 .
.
Доказательство:
Введем вспомогательную функцию 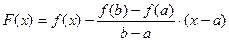 .
.
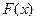 удовлетворяет условиям теоремы Роля (непрерывна, как разность двух непрерывных функций, дифференцируема).
удовлетворяет условиям теоремы Роля (непрерывна, как разность двух непрерывных функций, дифференцируема).
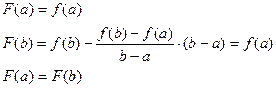
По теореме Роля 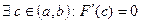
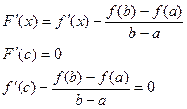
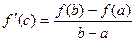 , ч.т.д.
, ч.т.д.
Геометрический смысл теоремы Лагранжа:
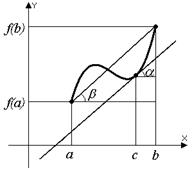
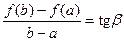
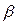 - угол наклона секущей, проходящей через точки
- угол наклона секущей, проходящей через точки 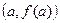 и
и 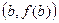 .
.
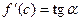 - угол наклона касательной в точке
- угол наклона касательной в точке 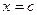 , т.е. внутри отрезка найдется точка, в которой касательная параллельна хорде, проходящей через точки
, т.е. внутри отрезка найдется точка, в которой касательная параллельна хорде, проходящей через точки 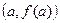 и
и 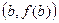 .
.
Формула конечных приращений Лагранжа.

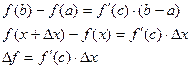
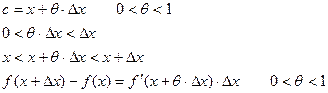
Т.4. Теорема Коши
Пусть:1) 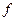 и
и 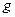 определены и непрерывны на отрезке
определены и непрерывны на отрезке 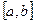
2) 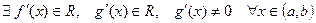
Тогда 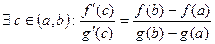 .
.
Доказательство:
Введем вспомогательную функцию 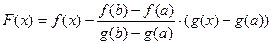 .
.
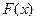 непрерывна и дифференцируема на
непрерывна и дифференцируема на 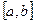 ,
, 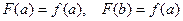 , т.е.
, т.е. 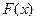 удовлетворяет условиям теоремы Роля, значит
удовлетворяет условиям теоремы Роля, значит
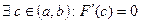
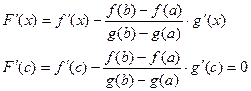
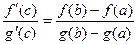 , ч.т.д.
, ч.т.д.
8.12. Правила Лопиталя.
Правила Лопиталя – правила для вычисления предела функции (раскрытие неопределенности 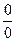 или
или 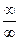 ).
).
Т.1. Пусть: 1) 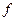 и
и 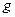 определены на
определены на 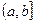
2) дифференцируемы на 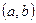 ,
, 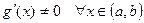
3) 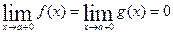
4) 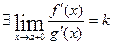
Тогда. 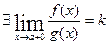 .
.
Доказательство: (по теореме Коши)
Доопределим 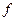 и
и 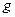 в точке
в точке 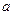 по непрерывности:
по непрерывности:
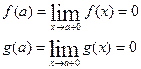
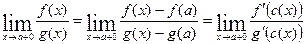
Замена: 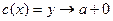 при
при 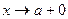 , тогда
, тогда
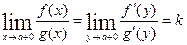 , ч.т.д.
, ч.т.д.
Т.2. Пусть: 1) 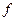 и
и 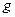 определены на
определены на 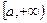
2) дифференцируемы на 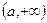 ,
, 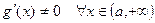
3) 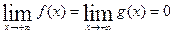
4) 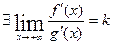
Тогда. 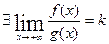 .
.
Доказательство:
Пусть 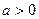 для определенности. Замена:
для определенности. Замена: 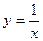 .
. 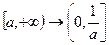
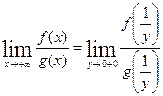 , по Т.1.
, по Т.1.
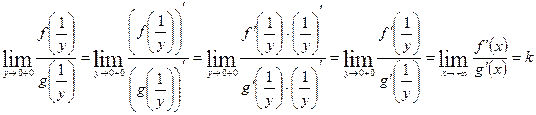 , ч.т.д.
, ч.т.д.
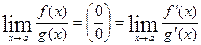 , где
, где 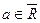
Т.3. Пусть: 1) 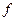 и
и 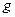 определены на
определены на 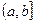
2) дифференцируемы на 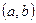 ,
, 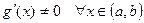
3) 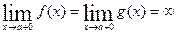
4) 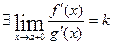
Тогда. 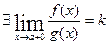 .
.
Пусть: 1) 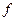 и
и 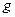 определены на
определены на 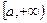
2) дифференцируемы на 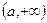 ,
, 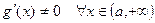
3) 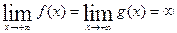
4) 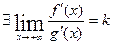
Тогда. 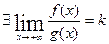 .
.
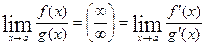 , где
, где 
Пример 1: 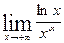 ,
, 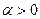
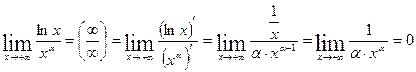
Степенная функция растет быстрее логарифмической при 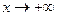 .
.
Пример 2: 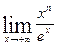
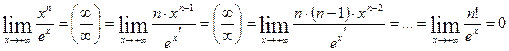
Показательная функция (при 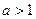 ) растет быстрее степенной при
) растет быстрее степенной при 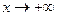 .
.
Пример 3: 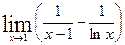
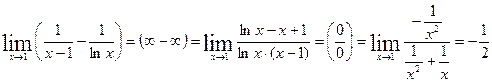
Пример 4: 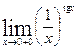
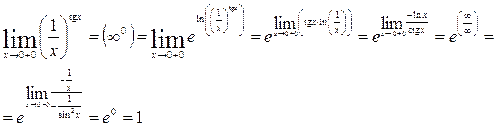
8.13. Формула Тейлора и Маклорена для многочлена.
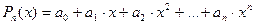
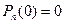
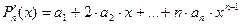
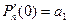
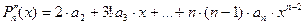
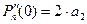
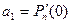 ,
, 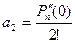 ,
, 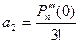 , …,
, …, 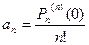 .
.
Коэффициенты многочлена выражаются через его значение и производные.
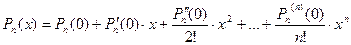 - формула Маклорена (разложение по степеням
- формула Маклорена (разложение по степеням 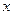 ).
).
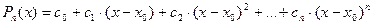
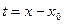
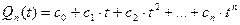
По формуле Маклорена:
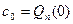 ,
, 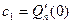 ,
, 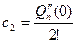 ,
, 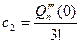 , …,
, …, 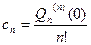 .
.
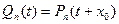
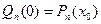
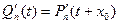
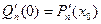
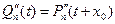
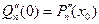 , …
, …
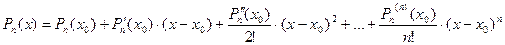 - формула Тейлора для многочлена (разложение по степеням
- формула Тейлора для многочлена (разложение по степеням 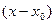 ).
).
8.14. Формула Тейлора и Маклорена для произвольной функции.
Пусть 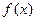 - функция такая, что у нее существуют производные
- функция такая, что у нее существуют производные 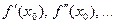 до
до 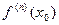 , т.е. все производные от 1 до
, т.е. все производные от 1 до 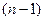 существуют в некоторой окрестности точки
существуют в некоторой окрестности точки  .
.
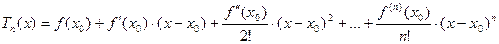 - многочлен Тейлора для функции
- многочлен Тейлора для функции 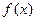 в точке
в точке  .
.
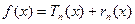 - формула Тейлора (
- формула Тейлора (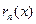 - остаточный член).
- остаточный член).
Формула Тейлора с остаточным в форме Пеано.
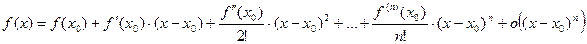 , при
, при 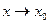
Доказательство:
Докажем, что 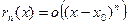 , при
, при 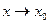 , т.е.
, т.е. 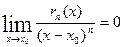 .
.
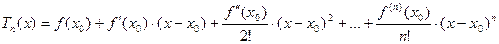
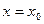
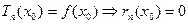
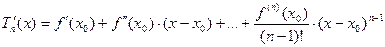
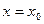
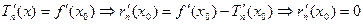 , …
, …
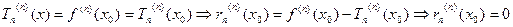
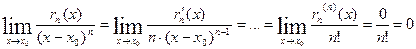 , ч.т.д.
, ч.т.д.
Для приложения формулы Тейлора нужны более конкретные формы.
Наложим на функцию более сильные ограничения.
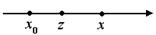 Пусть в некоторой окрестности точки
Пусть в некоторой окрестности точки  (
(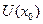 ) существуют
) существуют 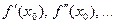
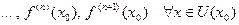 .
.
Возьмем 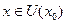 ,
, 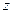 между
между  и
и 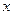 .
.
Составим функцию
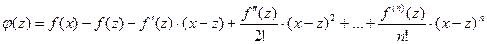
Вычислим 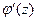 :
:
Выберем другую (произвольную) функцию  такую, чтобы она удовлетворяла условиям теоремы Коши в
такую, чтобы она удовлетворяла условиям теоремы Коши в  , и запишем теорему Коши для функций
, и запишем теорему Коши для функций 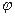 и
и 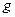 .
.
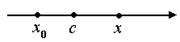
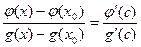 , где
, где 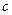 между
между  и
и 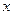 .
.
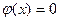
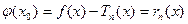
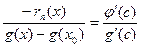
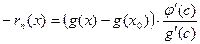
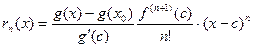
Подставляя разные функции  , получаем разные виды остаточного члена.
, получаем разные виды остаточного члена.
1) Остаточный член в форме Лагранжа.
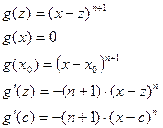
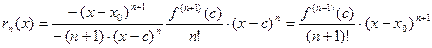
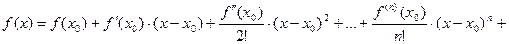
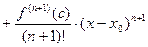 , где
, где 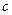 между
между  и
и 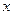 - формула Тейлора с остаточным членом в форме Лагранжа.
- формула Тейлора с остаточным членом в форме Лагранжа.
2) Остаточный член в форме Коши.
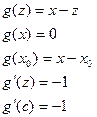
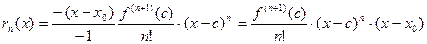
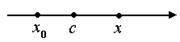
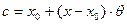 ,
, 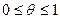
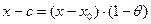
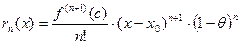
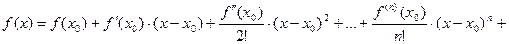
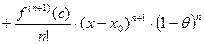 , где
, где 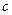 между
между  и
и 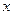 ,
, 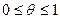 - формула Тейлора с остаточным членом в форме Коши.
- формула Тейлора с остаточным членом в форме Коши.
3) Остаточный член в форме Шлемильха и Роша.
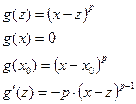
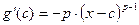
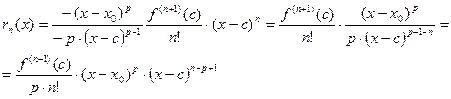
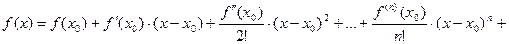
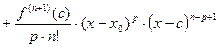 , где
, где 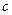 между
между  и
и 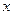 - формула Тейлора с остаточным членом в форме Шлемильха и Роша.
- формула Тейлора с остаточным членом в форме Шлемильха и Роша.
Многочлен Тейлора – многочлен наилучшего приближения для функции в окрестности точки  , т.е. из всех многочленов фиксированной степени в окрестности точки
, т.е. из всех многочленов фиксированной степени в окрестности точки  лучше всего функцию приближает именно многочлен Тейлора.
лучше всего функцию приближает именно многочлен Тейлора.
8.15. Разложение по формуле Тейлора (Маклорена) основных элементарных функций.
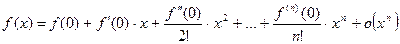 , при
, при 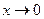
1) 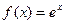
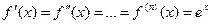
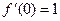
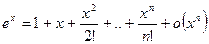 , при
, при 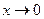 .
.
2) 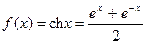
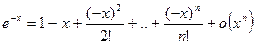
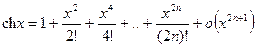 , при
, при 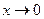 .
.
3) 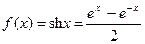
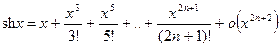 , при
, при 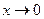 .
.
4) 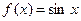
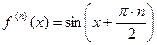
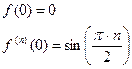
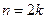
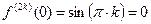
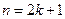
 2015-07-14
2015-07-14 528
528