Пример 1.6.4

Найдём рекуррентную формулу для вероятносте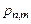й и 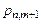появления ровно 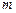и ровно 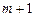успехов в серии из 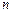испытаний по схеме Бернулли с вероятностью успеха .

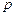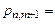
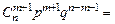
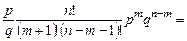
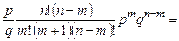
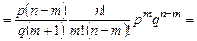
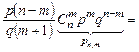
◄С помощью формулы Бернулли (1.6.1) находим: 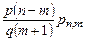. Итак,

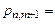
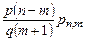(1.6.2)

- искомая рекуррентная формула.►

Пример 1.6.5.

Пусть 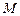- наиболее вероятное число успехов в серии из 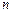испытаний по схеме Бернулли с вероятностью успеха 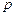. Покажем, что

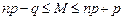. (1.6.3)

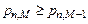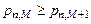◄По условию задачи и . Запишем формулу (1.6.2) для 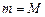и : ,

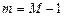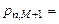
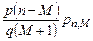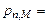
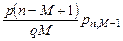
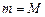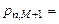
Запишем формулу (1.6.2) для : 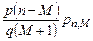. По условию 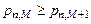, откуда получаем: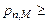 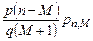или 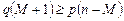, т.е. 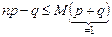. Первое из неравенств (1.6.3) доказано.

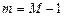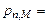
Запишем теперь формулу (1.6.2) для : 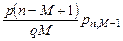, откуда 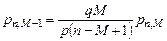. По условию 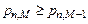, поэтому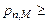 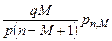или 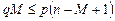, откуда получаем второе неравенство из (1.6.3). ►