Свойство 1. При перестановке пределов интегрирования определенный интеграл сохраняет свое абсолютное значение, но меняет знак на противоположный: 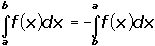
Например:
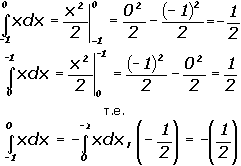
Свойство 2. При разбиении промежутка интегрирования исходный интеграл равен сумме интегралов по новым промежуткам интегрирования:
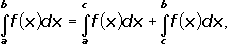
Например:
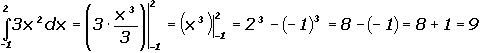
Одновременно:
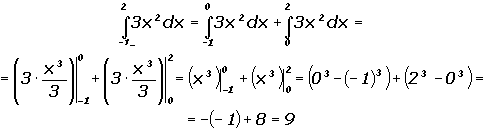
Остальные свойства определенного интеграла аналогичны свойствам не-определенного интеграла.
Свойство 3. Постоянный множитель можно выносить за знак интеграла:
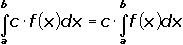
Свойство 4. Интеграл от алгебраической суммы равен алгебраической сумме интегралов от каждого слагаемого в отдельности:
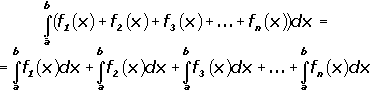
 2015-07-21
2015-07-21 355
355







