Линейные уравнения первого порядка. Метод Бернулли

Определение. Дифференциальное уравнение называется линейным относительно неизвестной функции и ее производной, если оно может быть записано в виде: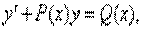

при этом, если правая часть Q(x) равна нулю, то такое уравнение называется линейным однородным дифференциальным уравнением, P(x) и Q(x)- функции непрерывные на некотором промежутке a < x < b.

Рассмотрим методы нахождения общего решения линейного однородного дифференциального уравнения первого порядка вида .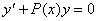

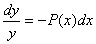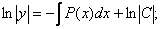Для этого типа дифференциальных уравнений разделение переменных производится по методу швейцарского математика Якоба Бернулли. Предположим: и тогда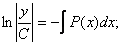

Отсюда общее решение: .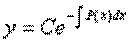

Суть метода заключается в том, что искомая функция представляется в виде произведения двух функций .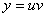

При этом очевидно, что 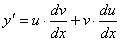и здесь будет необходимо дифференцирование по частям.

Подставляя в исходное уравнение, получаем:

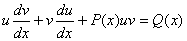
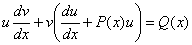
Т.к. первоначальная функция была представлена в виде произведения, то каждый из сомножителей, входящих в это произведение, может быть произвольным, выбранным по усмотрению математика.

Например, функция 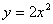может быть представлена как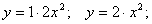

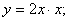и т.п.

Таким образом, можно одну из составляющих произведение функций выбрать так, что выражение .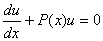

Таким образом, можно получить функцию u, проинтегрировав полученное соотношение как однородное дифференциальное уравнение по описанной выше схеме:

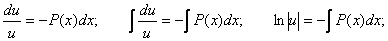
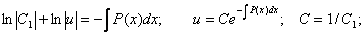
Для нахождения второй неизвестной функции v подставим поученное выражение для функции u в исходное уравнение 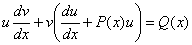с учетом того, что выражение, стоящее в скобках, равно нулю.

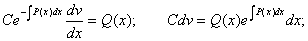
Интегрируя, можем найти функцию v:

; ;

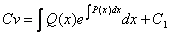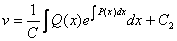Т.е. получена вторая составляющая произведения 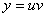, которое и определяет искомую функцию.

Подставляя полученные значения, получаем:

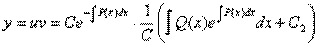
Окончательно получаем формулу:

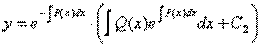, где С₂ - произвольный коэффициент.

Это соотношение считается решением неоднородного линейного дифференциального уравнения, полученным по способу Бернулли.