При расчетах эффективности осколочного действия необходимо знать число осколков, попавших в цель, которое зависит от характера распределения осколков в пространстве.
Закон разлета осколков определяется формой, которую приобретает оболочка к моменту ее разрушения и образования осколков. После разрушения оболочки каждый осколок, получив соответствующую начальную скорость, будет лететь в направлении движения того элемента оболочки, из которого он был образован.
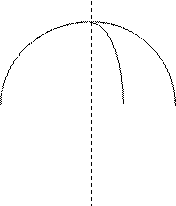
В системе координат, связанной с боевой частью, направление полета осколка принято определять двумя углами: углом j в меридиональной плоскости и углом q в экваториальной плоскости (рис.40).
 |
 j
j





 q
q
Рис.40
Полагают, что все осколки разлетаются из одной точки О – ц.м. боевой части. Так как все БЧ обладают осевой симметрией, то можно полагать, что в экваториальной плоскости осколки распределены равномерно.
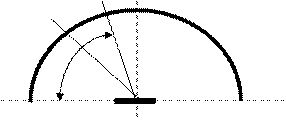
Чтобы охарактеризовать распределение осколков в пространстве, необходимо знать только распределение их в меридиональной плоскости, т.е. по углу j, которое можно определить опытным путем. Для этого подрывают БЧ в специальной мишенной обстановке (рис.41)..
|
|
|
 ji
ji
ji-1
Рис.41
На стенке наносят контур проекции части сферы между двумя меридиональными сечениями с углом Dq, которые определяют долю осколков, перехваченных мишенной обстановкой. На стеке наносят вертикальные линии, угловым секторам с шагом ji (рис.42).
 |
А B
 |
 j0 j1 ji-1 ji jm-1 jm
j0 j1 ji-1 ji jm-1 jm
Рис.42
Очевидно, что 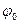 = 00,
= 00, 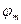 = 1800,
= 1800, 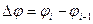 . После подрыва определяется количество осколков
. После подрыва определяется количество осколков 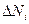 , попавших в каждый угловой сектор и общее число осколков
, попавших в каждый угловой сектор и общее число осколков 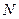 , перехваченных мишенью. Отношение
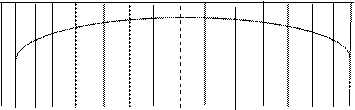
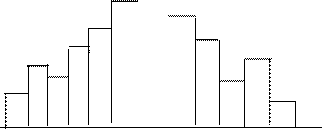
, перехваченных мишенью. Отношение 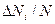 – статистическая вероятность того, что осколок полетит в данном угловом секторе и равно относительному количеству осколков, летящих в данном угловом секторе. Закон распределения осколков по направлению разлета представляется в виде гистограммы (рис.43)
– статистическая вероятность того, что осколок полетит в данном угловом секторе и равно относительному количеству осколков, летящих в данном угловом секторе. Закон распределения осколков по направлению разлета представляется в виде гистограммы (рис.43)

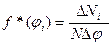
 |



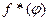
 |
j0 j1 j2 ji-1 ji jM
Рис.43
Площадь каждого прямоугольника гистограммы равна относительному числу осколков, летящих в данном угловом секторе. Общая площадь гистограммы равна 1.
Гистограмма строится по опытным данным, относящимся к угловому сектору Dq в экваториальной плоскости. Будем полагать, в силу симметрии БЧ, что она полностью характеризует закон распределения осколков по всей сфере.
Из рис.43 следует, что основная масса осколков летит в направлении, близком к нормали цилиндрической части оболочки.
Характерным показателем закона разлета является среднее направление разлета осколков
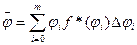

Для удобства расчетов распределения осколков по направлению разлета закон распределения можно представить в виде статистического интегрального закона (рис.44)
|
|
|
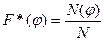
где 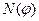 – число осколков, летящих в конусе с углом раствора 2
– число осколков, летящих в конусе с углом раствора 2 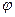 .
.
Очевидно, что 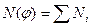 , где суммирование распространяется на те значения индекса i, для которых
, где суммирование распространяется на те значения индекса i, для которых 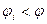 .
.












 Следовательно, интегральный закон представляет собой относительное число осколков, летящих в конусе с углом раствора
Следовательно, интегральный закон представляет собой относительное число осколков, летящих в конусе с углом раствора 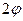 .
.


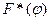 1
1


 |
j0 j1 j2 ji
Рис.44
Ординаты интегрального закона представляют собой сумму площадей прямоугольников гистограммы, расположенных левее точки 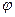 .
.
Гистограмму 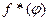 можно заменить непрерывной функцией
можно заменить непрерывной функцией 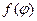 ,которая представляет собой дифференциальный закон распределения осколков по направлению разлета. Интегральный закон вычисляется по формуле
,которая представляет собой дифференциальный закон распределения осколков по направлению разлета. Интегральный закон вычисляется по формуле
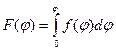
Пользуясь аналитическим выражением, или графиками законов в дифференциальной или интегральной формах можно определить число осколков, летящих ьежду двумя коническими поверхностями с углами раствора соответственно 2 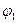 и 2
и 2 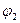 .
.
Вид закона распределения осколков по направлению разлета определяется в первую очередь формой оболочки и заряда. У оболочек цилиндрической формы основное количество осколков разлетается в узком секторе в направлении, примерно совпадающим с нормалью к поверхности оболочки. Еще более узкий сектор разлета можно получить у оболочек катушечной формы. У оболочек, имеющих выпуклую форму, угловой сектор увеличивается с увеличением кривизны (рис.45).

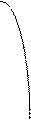
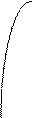

 f(j) катушка
f(j) катушка


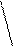 сфера цилиндр
сфера цилиндр
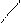








0 90 1800
Рис.45
У оболочек конической формы максимум закона распределения соответствует углам, примерно совпадающим к нормали поверхности оболочки. На вид закона распределения влияет расположение детонатора. Если точка инициирования на торце, то максимум распределения смещается в противоположную сторону на 5…15 град. В случае двухстороннего инициирования среднее направление разлета совпадает с нормалью к поверхности, угол раствора сектора разлета в этом случае будет существенно меньше. С увеличением коэффициента наполнения среднее направление разлета сдвигается в сторону больших углов, угол раствора сектора разлета увеличивается незначительно. Оболочки из хрупких материалов дают меньшие углы секторов разлета, чем из вязкого материала.
В действительности все боеприпасы имеют в момент разрыва собственную скорость (рис.46).
Vo Vo1




 K
K
B
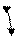
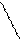
 j
j


 0 j1 A C
0 j1 A C


 V1
V1
 |
Рис.46
Собственная скорость в момент разрыва изменяет направление разлета осколков (уменьшает угловой сектор, в котором разлетаются осколки и сдвигает максимум закона разлета в сторону движения снаряда). Кроме того, наличие собственной скорости в момент разрыва приводит к некоторому увеличению начальной скорости осколка на траектории Из рис.46 с учетом собственной скорости осколка следует
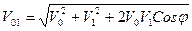
или
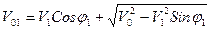
Если ввести относительную скорость w = V1/V0,то значение угла j1 можно получить из формулы
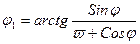
Пользуясь этой формулой можно получить, зная закон распределения осколков в неподвижных условиях, закон распределения, соответствующий скорости 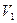 .
.
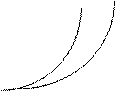
Допустим, что известен сглаженный интегральный закон распределения 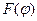 . Ордината закона распределения представляет собой относительное число осколков, летящих внутри конуса с углом раствора 2
. Ордината закона распределения представляет собой относительное число осколков, летящих внутри конуса с углом раствора 2 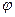 . Углу
. Углу 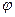 в случае разрыва движущейся БЧ будет соответствовать угол j1. Очевидно, что количество осколков в конусе с углом
в случае разрыва движущейся БЧ будет соответствовать угол j1. Очевидно, что количество осколков в конусе с углом 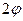 будет равно количеству осколков в конусе
будет равно количеству осколков в конусе 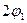 , т.е.
, т.е. 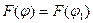 . Можно перестроить кривую
. Можно перестроить кривую 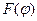 так, чтобы выполнялось условие
так, чтобы выполнялось условие 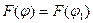 . Точка М1 в силу этого условия имеет ту же ординату, что и точка М. Таким образом можно определить закон разлета осколков
. Точка М1 в силу этого условия имеет ту же ординату, что и точка М. Таким образом можно определить закон разлета осколков 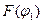 (рис.47).
(рис.47).




 F(j1), F(j)
F(j1), F(j)
M1 M
 |
j1 j 1800
Рис.47
 2015-07-14
2015-07-14 2247
2247








