Какие именно векторы создают фундаментальную систему решений данной системы уравнений?

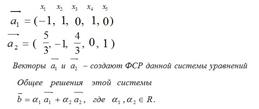
Пусть заданы линейные пространства и . Правило, по которому каждому элементу 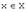ставится в соответствие единственный элемент 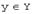, называется оператором, действующим в линейных пространствах . Результат действия оператора на элемент обозначают 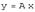или 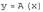. Если элементы и связаны соотношением 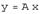, то называют образом элемента 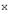; элемент 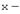прообразом элемента .

Множество элементов линейного пространства 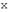, для которых определено действие оператора 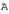, называют областью определения оператора и обозначают .

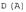Множество элементов линейного пространства , которые являются образами элементов из области определения оператора 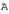, называют образом оператора и обозначают 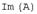. Если 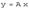, то .

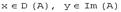Оператор 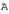, действующий в линейных пространствах 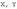называется линейным оператором, есл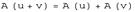и и для любых 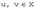и для любого числа .

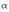Если пространства 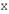и 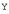совпадают, то говорят, что оператор действует в пространстве 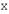. В дальнейшем ограничимся рассмотрением линейных операторов, действующих в линейном пространстве .