Линейная оболочка — это набор векторов, которые задают линейное подпространство. Строго говоря, линейная оболочка — это множество всех линейных комбинаций данных векторов. Так же обозначим особенности:
1) Если задана линейная оболочка — ранг набора векторов равен его размерности. С другой стороны в таком случае рангом или размерностью называют минимальное количество линейно независимых векторов в линейном подпространстве.
Задача: найдите ранг, размерность и базис набора векторов а₁ (2,4,1,0,-1), а₂ (1,-1,0,3,2), а₃ (3,9,2,-3,-4), а₄ (-1,7,1,-9,-7)
Решение: Выпишем матрицу и решим её методом Жордана-Гаусса:

Видим, что rank(A) = 2 (строчек две). Так как дана линейная оболочка, то dim(A) = rank(A) = 2
Итак, в базисе 2 вектора, так как dim(A) = 2. Мы должны выбрать 2 линейно-независимых вектора, которые входят в данное линейное подпространство. Для двух векторов линейная зависимость означает пропорциональность. Значит, выберем 2 непропорциональных вектора. Это, например, а₁ и а₂
Но если в базис бы входило 3 вектора? Пришлось бы опытным путём с помощью матрицы искать 3 линейно независимых.
Множество решений однородной линейной системы относительно n неизвестных является линейным подпространством пространства Rn. Размерность этого подпространства равна n − r, где r − ранг матрицы системы A.
Любой базис пространства решений однородной системы линейных уравнений называется фундаментальной системой решений однородной системы.
Иначе говоря, любая упорядоченная совокупность n − r линейно независимых решений однородной линейной системы образует фундаментальную систему решений однородной системы.
Однородная система линейных алгебраических уравнений
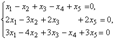
с помощью элементарных преобразований может быть приведена к каноническому виду:
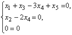
Ранг r матрицы равен 2, число n неизвестных равно 5, система нетривиально совместна. Размерность пространства решений этой однородной системы равна 3: d = n − I = 5 − 2 = 3.
три линейно независимые решения системы
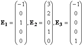
образуют базис пространства решений системы, т.е. образуют её фундаментальную систему решений.
 2015-07-14
2015-07-14 2260
2260
