Собственные значения и собственные векторы линейного оператора

Пусть 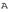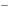линейный оператор, действующий в линейном пространстве.

Число 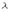называется собственным значением, а ненулевой вектор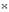 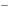соответствующим собственным вектором линейного оператора 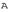, если они связаны между собой соотношением .

Пусть 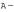матрица оператора в некотором базисе.

Собственные значения оператора и соответствующие им собственные векторы связаны соотношением 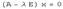, где 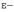единичная матрица, а нулевой элемент пространства 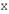. Это означает, что собственный вектор оператора является ненулевым решением линейной однородной системы 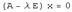, которое существует тогда и только тогда, когда 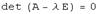. Следовательно, собственные значения линейного оператора могут быть вычислены как корни уравнения 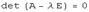, а собственные векторы -- как решения соответствующих однородных систем.

Уравнение 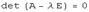называется характеристическим уравнением оператора, а многочлен 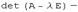характеристическим многочленом оператора.

Для собственных значений и собственных векторов линейного оператора справедливы следующие утверждения:

характеристический многочлен оператора, действующего в n-мерном линейном пространстве является многочленом n-й степени относительно ;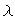

линейный оператор, действующий в n-мерном линейном пространстве имеет не более 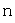различных собственных значений;

собственные векторы, отвечающие различным собственным значениям, линейно независимы;

если линейный оператор, действующий в n-мерном линейном пространстве 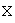, имеет 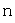различных собственных значений, то собственные векторы оператора образуют базис в пространстве 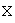; этот базис называют собственным базисом оператора;