Линейный оператор и его матрица. Переход к другому базису

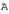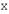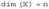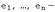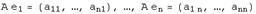Рассмотрим линейный оператор , действующий в конечномерном линейном пространстве , и пусть базис в . Обозначим через образы базисных векторов .

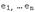Матрица

столбцами которой являются координаты образов базисных векторов, называется матрицей линейного оператора в заданном базисе.

Доказано, что каждому линейному оператору, действующему в n-мерном линейном пространстве, отвечает единственная квадратная матрица порядка n; и обратно 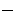каждая квадратная матрица порядка n задает единственный линейный оператор, действующий в этом пространстве. При этом соотношения

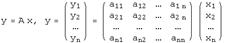
с одной стороны, связывают координаты образа 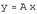с координатами прообраза 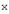, с другой стороны, описывают действие оператора, заданного матрицей .

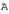При изменении базиса линейного пространства матрица оператора, очевидно, изменяется. Пусть в пространстве 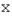произошел переход от базиса 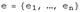к базису 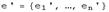. Связь между матрицей оператора в базисе и матрицей этого оператора в базисе 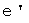задается формулой.

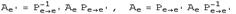
Здесь 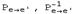матрица перехода от базиса к базису и обратная к ней.