Дифракция света. Принцип Гюйгенса-Френеля. Дифракция Френеля и Фраунгофера. Метод зон Френеля. Дифракция на круглом отверстии и диске

Дифракция – огибание светом препятствия, проникновение света в область геометрической тени.

Принцип Гюйгенса—Френеля: Каждый элемент волнового фронта можно рассматривать как центр вторичного возмущения, порождающего вторичные сферические волны, а результирующее световое поле в каждой точке пространства будет определяться интерференцией этих волн.

Дифракция Френеля:

На рисунке изображён непрозрачный экран с круглым отверстием, на некотором расстоянии от которого расположен источник света. Изображение фиксируется на другом экране справа. Вследствие дифракции свет, проходящий через отверстие, расходится. Поэтому область, которая была затенена по законам геометрической оптики, будет частично освещённой. В области, которая при прямолинейном распространении света была бы освещённой, наблюдаются колебания интенсивности освещения в виде концентрических колец.

Дифракция Фраунгофера:

Случай дифракции, при котором дифракционная картина наблюдается на значительном расстоянии от отверстия или преграды. Иными словами, дифракция Фраунгофера наблюдается тогда, когда число зон Френеля 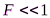, при этом приходящие в точку волны являются практически плоскими. При наблюдении данного вида дифракции изображение объекта не искажается и меняет только размер и положение в пространстве. В противоположность этому, при дифракции Френеля изображение меняет также свою форму и существенно искажается.

Метод зон Френеля:

Зоны Френеля - участки, на которые можно разбить поверхность световой волны для вычисления результатов дифракции света.

Суть метода такова. Пусть от светящейся точки распространяется сферическая волна и требуется определить характеристики волнового процесса, вызванного ею в точке 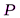. Разделим поверхность волны 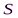на кольцевые зоны. Для этого проведём из точки 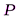сферы радиусами 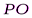, , 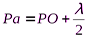, 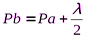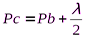( — точка пересечения поверхности волны с линией ). Кольцеобразные участки поверхности волны, «вырезаемые» из неё этими сферами, и называется зонами Френеля. Волновой процесс в точке 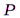можно рассматривать как результат сложения колебаний, вызываемых в этой точке каждой зоной Френеля в отдельности.

Дифракция Френеля на круглом отверстии:

С 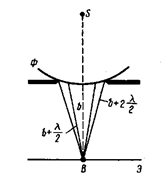ферическая волна, распространяющаяся из точечного источника , встречает на своем пути экран с круглым отверстием. Дифракционная картина наблюдается на экране в точке 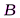. Разобьем часть волновой поверхности 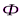на зоны Френеля. Вид дифракционной картины будет зависеть от количества зон Френеля, укладывающихся в отверстии. Амплитуда результирующего колебания в точке 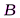равна: 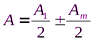(плюс для нечетных , минус – для четных). Дифракционная картина от круглого отверстия вблизи точки 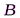будет иметь вид чередующихся светлых и темных колец.

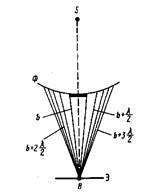
Дифракция Френеля на диске:

Сферическая волна, распространяющаяся из точечного источника 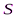, встречает на своем пути диск. Дифракционная картина наблюдается на экране 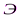в точке 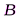. Пусть диск закрывает 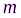первых зон Френеля. Тогда амплитуда результирующего колебания в точке 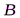равна: 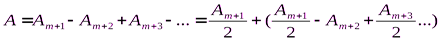. Т.к. слагаемое в скобках равно 0, то 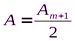. Следовательно, в точке всегда будет светлое пятно, окруженное концентрическими светлыми и темными кольцами, а интенсивность убывает с расстоянием от центров картины.

44) Дифракционная решетка

Дифракционная решётка — оптический прибор, действие которого основано на использовании явления дифракции света. Представляет собой совокупность большого числа регулярно расположенных штрихов (щелей, выступов), нанесённых на некоторую поверхность. Первое описание явления сделал Джеймс Грегори, который использовал в качестве решётки птичьи перья.

Расстояние, через которое повторяются штрихи на решётке, называют периодом дифракционной решётки. Обозначают буквой d.

Если известно число штрихов (), приходящихся на 1 мм решётки, то период решётки находят по формуле: 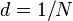мм.

Условия интерференционных максимумов дифракционной решётки, наблюдаемых под определёнными углами, имеют вид:

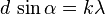
где

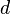— период решётки,

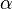— угол максимума данного цвета,

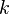— порядок максимума, то есть порядковый номер максимума, отсчитанный от центра картинки,

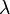— длина волны.

Если же свет падает на решётку под углом 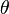, то:

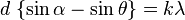
Одной из характеристик дифракционной решётки является угловая дисперсия. Предположим, что максимум какого-либо порядка наблюдается под углом φ для длины волны λ и под углом φ+Δφ — для длины волны λ+Δλ. Угловой дисперсией решётки называется отношение D=Δφ/Δλ. Выражение для D можно получить если продифференцировать формулу дифракционной решётки

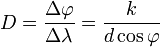
Таким образом, угловая дисперсия увеличивается с уменьшением периода решётки d и возрастанием порядка спектра k.

45) Дисперсия света

Диспе?рсия све?та (разложение света) — это явление, обусловленное зависимостью абсолютного показателя преломления вещества от частоты (или длины волны) света (частотная дисперсия), или, то же самое, зависимость фазовой скорости света в веществе от длины волны (или частоты). Экспериментально открыта Ньютономоколо 1672 года, хотя теоретически достаточно хорошо объяснена значительно позднее.

• Пространственной дисперсией называется зависимость тензора диэлектрической проницаемости среды от волнового вектора. Такая зависимость вызывает ряд явлений, называемых эффектами пространственной поляризации.

Один из самых наглядных примеров дисперсии — разложение белого света при прохождении его через призму (опыт Ньютона). Сущностью явления дисперсии является различие фазовых скоростей распространения лучей света c различной длиной волны в прозрачном веществе — оптической среде (тогда как в вакууме скорость света всегда одинакова, независимо от длины волны и следовательно цвета). Обычно, чем больше частота световой волны, тем больше показатель преломления среды для неё и тем меньше фазовая скорость волны в среде:

• у света красного цвета фазовая скорость распространения в среде максимальна, а степень преломления — минимальна,
• у света фиолетового цвета фазовая скорость распространения в среде минимальна, а степень преломления — максимальна.

Однако в некоторых веществах (например в парах иода) наблюдается эффект аномальной дисперсии, при котором синие лучи преломляются меньше, чем красные, а другие лучи поглощаются веществом и от наблюдения ускользают. Говоря строже, аномальная дисперсия широко распространена, например, она наблюдается практически у всех газов на частотах вблизи линий поглощения, однако у паров иода она достаточно удобна для наблюдения в оптическом диапазоне, где они очень сильно поглощают свет.

Дисперсия света позволила впервые вполне убедительно показать составную природу белого света.

• Белый свет разлагается в спектр и в результате прохождения через дифракционную решётку или отражения от неё (это не связано с явлением дисперсии, а объясняется природой дифракции). Дифракционный и призматический спектры несколько отличаются: призматический спектр сжат в красной части и растянут в фиолетовой и располагается в порядке убывания длины волны: от красного к фиолетовому; нормальный (дифракционный) спектр — равномерный во всех областях и располагается в порядке возрастания длин волн: от фиолетового к красному.

По аналогии с дисперсией света, также дисперсией называются и сходные явления зависимости распространения волн любой другой природы от длины волны (или частоты). По этой причине, например, термин закон дисперсии, применяемый как название количественного соотношения, связывающего частоту и волновое число, применяется не только к электромагнитной волне, но к любому волновому процессу.

Дисперсией объясняется факт появления радуги после дождя (точнее тот факт, что радуга разноцветная, а не белая).

Дисперсия является причиной хроматических аберраций — одних из аберраций оптических систем, в том числе фотографических и видео-объективов.

Огюстен Коши предложил эмпирическую формулу для аппроксимации зависимости показателя преломления среды от длины волны:

,

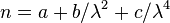где 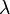— длина волны в вакууме; a, b, c — постоянные, значения которых для каждого материала должны быть определены в опыте. В большинстве случаев можно ограничиться двумя первыми членами формулы Коши. Впоследствии были предложены другие более точные, но и одновременно более сложные, формулы аппроксимации.

46) Поляризация света. Закон Малюса.

Испускание кванта света происходит в результате перехода электрона из возбужденного состояния в основное. Электромагнитная волна, испускаемая в результате этого перехода, является поперечной, то есть вектора и 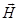взаимно перпендикулярны и перпендикулярны направлению распространения. Колебания вектора происходят в одной плоскости. Свет, в котором вектор колеблется только в одном направлении, называется плоско поляризованным светом (или электромагнитной волной). Поляризованным называется свет, в котором направления колебания вектора упорядочены каким-либо образом.

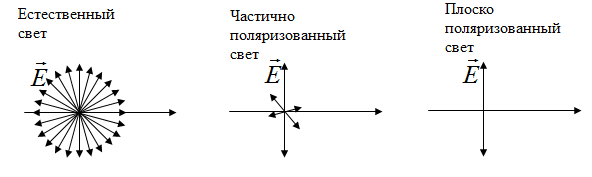
Свет представляет собой суммарное электромагнитное излучение множества атомов. Атомы излучают световые волна независимо друг от друга, поэтому световая волна, излучаемая телом в целом, харак­теризуется всевозможными равновероятными колебаниями светового вектора . Свет со всевозможными равновероятными ориентациями вектора называется естественным. Свет, в котором имеется преимущественное направление колебаний вектора и незначительная амплитуда колебаний вектора в других направлениях, называется частично поляризованным. В плоско поляризованном свете плоскость, в которой колеблется вектор ,называется плоскостью поляризации, плоскость, в которой колеблется вектор 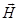, называется плоскостью колебаний.

Вектор называют световым вектором потому, что при действии света на вещество основное значение имеет электрическая составляющая поля волны, действующая на электроны в атомах вещества.

Различает также эллиптически поляризованный свет: при распростра­нении электрически поляризованного света вектор описывает эллипс, и циркулярно поляризованный свет (частный случай эллиптически поляризованного света) - вектор описывает окружность (сравните со сложением взаимно перпендикулярных колебаний: возможны: прямая линия, эллипс и окружность).

Степенью поляризации называется величина

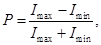
где I_max и I_min – максимальная и минимальная компоненты интенсивности света, соответствующие двум взаимно перпендикулярным компонентам вектора (то есть Е_х и Е_у – составляющие). Для плоско поляризованного света Е_у = Е, Е_х = 0, следовательно, Р = 1. Для естественного света Е_у = Е_х = Е и Р = 0. Для частично поляризованного света Е_у = Е, Е_х = (0...1) Еу, следовательно, 0 < Р < 1.

Если вектор в эллиптически поляризованном свете вращается при распространении света по часовой стрелке, то поляризация называется правой, против - левой. В эллиптически поляризованном свете колебания полностью упорядочены. К эллиптически поляризованному свету понятие степени поляризации не применимо, так что Р=1 всегда.