В зависимости от угла между пересекающимися осями коническая зубчатая передача может быть ортогональной (межосевой угол 90°) и неортогональной (межосевой угол S = 10° ¸ 170°, но ¹ 90°). Учитывая, что в подвижном составе находят применение только ортогональные передачи, ограничимся рассмотрением этих передач.
Передаточное отношение передачи определяется отношением абсолютных величин угловых скоростей колес
i 12 = ï`w1ï / ï`w2ï = sin dw2 / sin dw1 = ctg dw1 (6.35)
где dw1, sin dw2 - углы начальных конусов.
В ортогональной передаче
dw2 = 90° - dw1 (6.36)
Кратко рассмотрим особенности геометрии конических колес и связанные с ними преобразования расчётных формул.
Вместо начальных и делительных цилиндров (в плоском сечении окружностей) цилиндрических колес здесь вводятся понятия: начальный и делительный конусы, которые как правило совпадают.
По признаку изменения размеров сечения по длине зуба ГОСТ 19326-73 предусматривает 3 формы зубьев.
Мы рассмотрим только одну - основную для прямозубых и косозубых конических передач. Это форма I, при которой зубья нормально понижаются, вершина начального и внутреннего конусов совпадают. У этих колес обычно выбирают стандартные значения внешнего окружного модуля m te и определяют размеры зуба на внешнем торце, на котором удобно производить измерения.
Рассмотрим формулы для расчёта основных геометрических размеров конических зубчатых колес с прямыми зубьями (рис.6.25).
Внешнее конусное расстояние
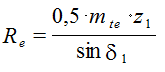 (6.37)
(6.37)
Диаметр внешней делительной окружности
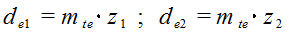 (6.38)
(6.38)
Ширина венца
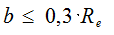 (6.39)
(6.39)
Среднее конусное расстояние
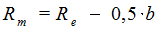 (6.40)
(6.40)
Наибольшая высота зубьев (у торца)
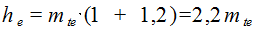 (6.41)
(6.41)
Окружная толщина зуба по внешней делительной окружности
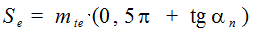 (6.42)
(6.42)
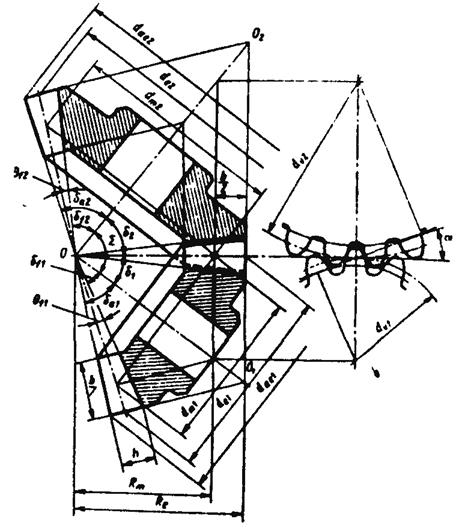
Рис.6.25
Угол делительного конуса
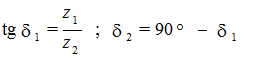 (6.43)
(6.43)
Нормальный модуль в середине ширины венца
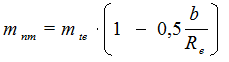 (6.44)
(6.44)
Используя метод дополнительных конусов, конические колеса эаменяют эквивалентными цилиндрическими, диаметр начальной окружности и модуль которых равны диаметру начальной окружности и модулю в среднем сечении зуба конических колес, а профиль зубьев соответствует профилю эквивалентных колес.
Эквивалентная цилиндрическая передача - эвольвентная цилиндрическая зубчатая передача, размеры и форма зубьев зубчатых колес которой в главном сечении практически идентичны размерам и форме зубьев колес конической зубчатой передачи в сечении их начальными дополнительными конусами.
На рис 6.26. обозначены: 1 и 2 — зубчатые колеса конической передачи, 4 и 3 — соответственно их дополнительные конусы в заданном сечении, r wvt1 и r wvt2 — начальные радиусы соответственно эквивалентных шестерни и колеса, которые равны длинам образующих начальных дополнительных конусов шестерни и колеса конической зубчатой передачи, соответствующих заданному начальному конусному расстоянию.
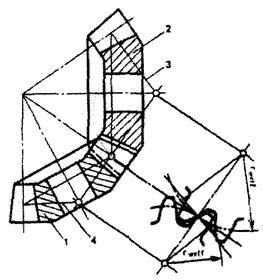
Рис.6.26
Диаметры эквивалентных колес:
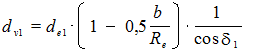 (6.45)
(6.45)
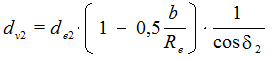 (6.46)
(6.46)
Эквивалентное число зубьев прямозубых колес:
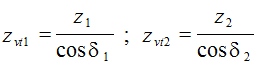 (6.47)
(6.47)
Биэквивалентное число зубьев косозубых колес:
Zvn1= Z1/cosd1cos3bm; Zvn2=Z2/cosd2 cos3bm; (6.48)
Эквивалентное передаточное отношение:
Uv = dv2/dv1 = U2 (6.49) 
 2015-07-14
2015-07-14 1366
1366
