Конические зубчатые передачи применяют при пересекающихся (см. рис. 3.2, д, е, ж) или скрещивающихся осях (см. рис.3.2, з — гипоидная передача). Межосевой угол 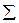 может изменяться в широком диапазоне значений (10° <
может изменяться в широком диапазоне значений (10° < 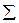 < 170°), но наибольшее распространение имеют ортогональные конические передачи с углом
< 170°), но наибольшее распространение имеют ортогональные конические передачи с углом 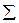 = 90°.
= 90°.
Конические зубчатые передачи по сравнению с цилиндрическими имеют большую массу и габариты, сложнее в изготовлении, а также монтаже, так как требуют точной фиксации осевого положения зубчатых колес.
Наибольшее распространение имеют конические передачи с прямыми и криволинейными зубьями; последние постепенно вытесняют передачи с тангенциальными зубьями (см. рис.3.2, д, е, ж). Конические зубчатые колеса с криволинейными зубьями могут иметь круговую, эвольвентную и циклоидальную линию зубьев; наиболее распространенные колеса с круговыми зубьями.
Конические передачи с криволинейными зубьями по сравнению с прямозубыми имеют большую нагрузочную способность, работают более плавно и, следовательно, динамические нагрузки и шум при их работе меньше. Допуски для конических и гипоидных передач регламентированы стандартом, согласно которому установлено двенадцать степеней точности и соответствующие нормы точности.
Предельные окружные скорости для конических прямозубых (непрямозубых) колес имеют следующие величины: при 6-й степени точности — до 12 (20) м/с, 7-й степени — до 8 (10) м/с, 8-й степени — до 4 (7) м/с, 9-й — до 1,5 (3) м/с.
Расчет геометрии конических прямозубых передач регламентирован ГОСТом. На рис. 3.22 показаны основные геометрические параметры прямозубого цилиндрического колеса: Re, R — внешнее и среднее конусное расстояния; b — ширина зубчатого венца; d, de — средний и внешний
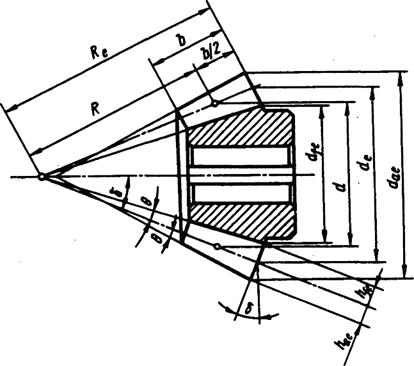 Рис. 3.22
Рис. 3.22
делительный диаметры; dae, d fe — внешние диаметры вершин зубьев и впадин; 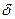 — угол делительного конуса; hас, h fe — внешняя высота делительной головки и ножки зуба;
— угол делительного конуса; hас, h fe — внешняя высота делительной головки и ножки зуба; 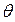 а =
а = 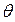 f =
f = 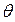 — угол делительной головки и ножки зуба.
— угол делительной головки и ножки зуба.
Углы головки и ножки зуба сделаны одинаковыми для того, чтобы образующая конуса вершин зубьев одного колеса была параллельна образующей конуса впадины второго колеса, в результате чего радиальный зазор по длине прямого зуба будет постоянным (поэтому на рис. 3.22 вершины конусов не совпадают).
По приведенным выше параметрам определяют остальные размеры колес и передачи, в частности:
угол конуса вершин зубьев
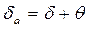 ; (3.37)
; (3.37)
угол конуса впадин
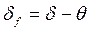 (3.38)
(3.38)
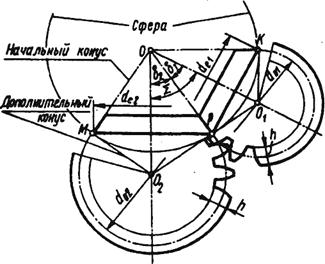
межосевой угол передачи (рис. 3.23)
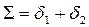 (3.39)
(3.39)
У конических колес высота, толщина зубьев и окружной шаг по длине зуба неодинаковы, поэтому различают два окружных модуля:
m — средний делительный окружной модуль, причем d = mz, где z — число зубьев колеса;
me — внешний делительный окружной модуль, причем de = mez.
Внешний и средний модули пропорциональны соответствующим конусным расстояниям, поэтому
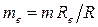 .
.
Для удобства измерений на чертежах задают внешние размеры зубьев и колес, а модуль те называют производственным, который обычно (но не обязательно) слндует округлить до стандартного значения.
Рис.3.23
Существуют нормальные внешний и средний модули тne и тп.
Профилирование зубьев конических колес с прямыми и тангенциальными, а также колес с круговыми зубьями ведется в соответствии со стандартами на соответствующие исходные контуры. Исходный контур для прямозубых конических колес аналогичен исходному контуру для цилиндрических колес (см. рис. 3.11), за исключением радиального зазора с = 0,2те; внешняя высота головок зубьев пж = те, внешняя высота но жек hfe =1,2те, а внешняя высота зуба ha = 2,2те.
Внешний диаметр вершин зубьев равен
dae = de + 2hm cosδ = me(z + 2cosδ). (3.40)
Очевидно, что при Σ = 90°
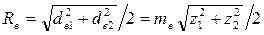 . (3.41)
. (3.41)
а также
Re = d/(2smδ), R = Re-b/2. (3.42)
Углы делительных конусов ортогональных передач легко определяются в зависимости от числа зубьев ведущего и ведомого колес, а следовательно, от передаточного числа передачи:
tgδ1 = d1/d2 = z1/z2 = 1/и или и = ctgδ1, = tgδ2. (3.43)
Ширину зубчатого венца b по стандарту рекомендуется принимать
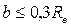 или
или 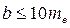 ; (3.44)
; (3.44)
вычисленное значение округляется до целого числа, а при проектировании стандартных редукторов значения b принимаются по стандарту.
Кроме ширины венца b указанный стандарт на ортогональные конические передачи для редукторов устанавливает номинальные значения внешнего делительного диаметра колеса de2 (в основном определяющего габариты редуктора) и номинальные значения передаточных чисел и (от и = 1 до и = 6,3, см. табл. 3.6). В приложении к ГОСТу имеется таблица, в которой для каждого стандартного значения передаточного числа и указаны взаимно согласованные значения de2 и b.
Для прямозубых конических передач рекомендуется и < 3, для передач с криволинейными зубьями и < 6,3; число зубьев меньшего колеса рекомендуется z1 = 18-30.
Эквивалентные колеса.
Зубья конических колес профилируют по эвольвенте так же, как и зубья цилиндрических, но коническая передача является пространственной и поэтому точки ее сопряженных профилей лежат на сферической поверхности, которая не развертывается на плоскость. Поэтому профилирование зубьев конических колес с незначительной погрешностью выполняется на поверхности дополнительных конусов (см. Рис. 3.23) которые, мысленно разрезав по образующей, можно развернуть на плоскости.
Образующие дополнительных конусов перпендикулярны образующим делительных конусов, поэтому диаметры воображаемых прямозубых цилиндрических колес, называемые эквивалентными колесами, определяются по формулам
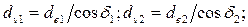 (3.45)
(3.45)
где d1 и d2 — углы делительных конусов конических колес.
Числа зубьев эквивалентных колес, называемые эквивалентными числами зубьев, равны
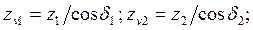 (3.46)
(3.46)
где z\ и z2 — действительные числа зубьев конических колес.
Эквивалентным числом зубьев пользуются при определении коэффициента формы зуба по табл. 3.8
Силы в конической передаче. При силовом расчете конических передач полагают, что равнодействующая сил нормального давления Fn приложена в среднем сечении зуба, а силами трения, как и ранее, пренебрегают. Разложим силу Fn на три взаимно перпендикулярные составляющие по реальным направлениям (рис. 3.24), в результате чего получим:
окружная сила на шестерне и колесе
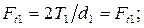 (3.47)
(3.47)
радиальная сила на шестерне, численно равная осевой силе на колесе,
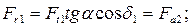 (3.48)
(3.48)

осевая сила на шестерне, численно равная радиальной силе колеса
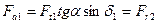 . (3.49)
. (3.49)
Расчет зубьев конической передачи на контактную усталость.
Критерии работоспособности и методика расчетов на прочность конических и цилиндрических передач аналогичны. Поэтому расчет зубьев конических передач сводится к расчету зубьев эквивалентной цилиндрической тередачи с учетом установленного опытным путем коэффициента понижения нагрузочной способности конической передачи, равного 0,85.
Модуль зубьев эквивалентного цилиндрического колеса принимается для прочностных расчетов равным модулю т в среднем сечении зуба, а диаметр делительной окружности
эквивалентного колеса принимают равным диаметру среднего дополнительного конуса; эквивалентное число зубьев будет определяться по ранее выведенным формулам, а передаточное число эквивалентных колес uv будет равно
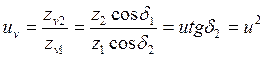 ,
,
так как при 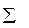 = 90° cosδ, = sinδ2, a tgδ2 = и.
= 90° cosδ, = sinδ2, a tgδ2 = и.
Подставив в ранее выведенную формулу для проверочного расчета цилиндрических колес параметры эквивалентного колеса
(uv = и2, dvl = d1/cosδ1 =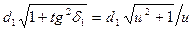 ),
),
а также введя коэффициент понижения нагрузочной способности, равный 0,85, получим формулу для проверочного расчета зубьев конических прямозубых передач на контактную усталость:
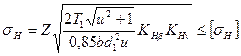 , (3.50)
, (3.50)
где Z = 462-103 Па1/2 для стальных колес.
Формула для проектного расчета прямозубых конических передач на контактную прочность выглядит следующим образом:
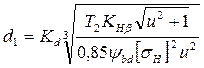 (3.51)
(3.51)

где для предварительных расчетов стальных колес Kd = 7700 Па1/3,
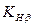
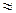 1,3, коэффициент ширины колеса относительно среднего диаметра шестерни
1,3, коэффициент ширины колеса относительно среднего диаметра шестерни 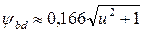 .
.
Поскольку основным размером, определяющим габариты конической передачи, является внешний диаметр колеса, то формулу для проектного расчета прямозубых передач можно преобразовать и использовать в следующем виде:
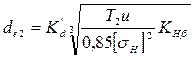 (3.52)
(3.52)
Здесь de2 — внешний делительный диаметр колеса (de2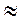 l,17d2 =1,17d1u); K'd = 16 500 Па1/3 для стальных колес.
l,17d2 =1,17d1u); K'd = 16 500 Па1/3 для стальных колес.
Расчет зубьев конической передачи на усталость при изгибе. Основным видом проектного расчета закрытых конических передач с низкой и средней твердостью зубьев является расчет на контактную усталость активных поверхностей зубьев, а расчет на усталость зубьев при изгибе применяется как проверочный. Исключением являются передачи с высокой твердостью активных поверхностей зубьев (Н > 50 HRC3, их нагрузочная способность лимитируется изгибной прочностью); параметры таких передач определяют из расчета зубьев на изгиб, причем основным расчетным параметром является модуль.
Проектным расчетом открытых передач также является расчет на усталость зубьев при изгибе.
Формула проверочного расчета на изгиб прямозубых конических передач имеет вид
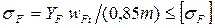 (3.53)
(3.53)
где YF — коэффициент формы зуба, определяемый по табл. 3.8 по эквивалентному числу зубьев zv; параметр wFt = 2T1KFβKFv/(d1b); m — средний модуль.
Формула проектного расчета на изгиб прямозубых конических передач имеет вид
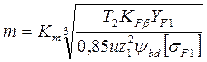 , (3.54)
, (3.54)
где Кm = 1,4; коэффициент неравномерности нагрузки КFβ определяется по графику на рис. 3.19; числом зубьев шестерни задаются, обычно z, = 18-30; ум «0,166v и2 +1 (расчет ведется по шестерне).
По найденной величине среднего модуля определяется производственный модуль me, который можно округляют до стандартного значения по табл.3.1.
Допускаемые напряжения для расчетов конических передач определяются так же) как для цилиндрических.
Конические передачи с тангенциальными и криволинейными зубьями приближенно рассчитывают по тем же формулам, что и прямозубые, но по нормальному среднему модулю и с введением в знаменатель подкоренного выражения коэффициента Кk, учитывающего большую прочность этих зубьев. На основании опытных данных КHk = 1,5 — при расчетах зубьев на контактную усталость; KFk = 1,0 — при расчетах зубьев на изгиб. Коэффициент Кk вводится вместо коэффициента 0,85.
Для обеспечения примерной равнопрочности зубьев на контактную усталость и изгиб внешний окружной модуль можно ориентировочно определять по формуле
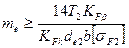 (3.55)
(3.55)
(для прямозубых передач КFk = 0,85).
Коэффициент формы зуба для криволинейных зубьев определяется по табл. 3.8 по биэквивалентному числу зубьев
zv = z/(cosδ-cos3β),
полученному двойным приведением: конического колеса к цилиндрическому и криволинейного зуба к прямому.
 2014-02-02
2014-02-02 8704
8704
