Формула Виллиса выводится на основании основной теоремы зубчатого зацепления и устанавливает соотношение между угловыми скоростями зубчатых колес в планетарном механизме. Рассмотрим простейший планетарный механизм с одним внешним зацеплением (см. рис.6.28). Число подвижностей в этом механизме равно
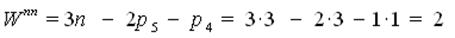
то есть для получения определенности движения звеньев механизма необходимо сообщить независимые движения двум его звеньям. Рассмотрим движение звеньев механизма относительно стойки и относительно водила.
Чтобы записать передаточное отношение планетарного механизма через число зубьев, применим метод обращения движения (как бы искусственно обратим планетарный механизм в механизм с неподвижной осью О 2). Для этого мысленно сообщим всем звеньям механизма, включая стойку, дополнительное движение с угловой скоростью - wн. Получим обращенный планетарный механизм с неподвижными осями зубчатых колес.
Таблица 6.1 - Типовые планетарные механизмы
| № | Структурная схема механизма | Рекомендуемое Uред |
| 1. | 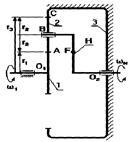 | 3… 10 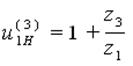 |
| 2. | 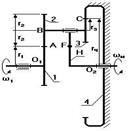 | 7… 16 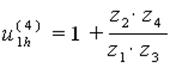 |
| 3. | 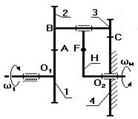 | 25… 300 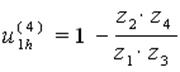 |
| 4. | 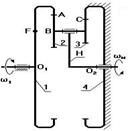 | 30… 300 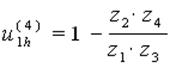 |
|
|
|
Движение звеньев механизма относительно стойки
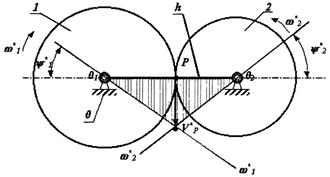
Движение звеньев механизма относительно водила
Рис. 6.28
В обращенном движении звенья этого механизма будут иметь следующие угловые скорости:
w1* = w1 – wн
w2* = w2 + (–wн) = w2 – wн
wн* = wн – wн = 0
В движении звеньев относительно водила угловые скорости звеньев равны угловым скоростям в движении относительно стойки минус угловая скорость водила.
Угловые скорости звеньев в каждом из рассматриваемых движений приведены в таблице 6.2.
Таблица 6.2
| Движение механизма | Звено 1 | Звено2 | Звено h | Звено 0 |
| Относительно стойки | w1 | w2 | wh | w0 = 0 |
| Относительно водила | w*1= w1- wh | w*2 =w2- wh | wh- wh = 0 | -wh |
Если в движении относительно стойки ось зубчатого колеса 2 подвижна, то в движении относительно водила оси обоих зубчатых колес неподвижны. Поэтому к движению относительно водила можно применить основную теорему зацепления.
То есть можно записать выражение, которое называется формулой Виллиса для планетарных механизмов
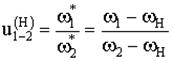 (6.62)
(6.62)
6.8.3. Определение передаточного отношения планетарных механизмов различных схем.
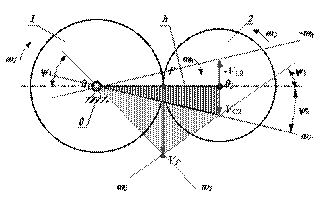
Планетарный однорядный механизм (рис.6.29)
(механизм Джеймса).
Графический способ определения передаточного отношения.
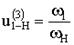
Выберем на водиле Н точку F которая расположена на том же расстоянии от оси О 2, что и точка А.
Оси О 1 и О 2 расположены на одном уровне.
Для данной схемы входное звено – звено 1 (солнечное колесо), выходным является водило Н.
Зададимся отрезком АА ’, который изображает линейную скорость колеса 1 в точке А. Т.к. колесо 1 вращается вокруг О 1, то закон распределения линейной скорости по первому звену изображается прямой линией О 1 А ’. Сателлит 2 в точке А имеет такую же линейную скорость, что и колесо 1. В точке С сателлит 2 имеет мгновенный центр скоростей (МЦС) в абсолютном движении, т.к. идет контакт с неподвижным колесом 3. Закон распределения линейной скорости по второму колесу изображается прямой линией СА ’.
|
|
|
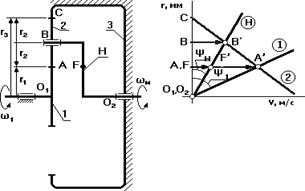
Рис.6 29.
В точке В сателлит имеет линейную скорость, которая изображается отрезком ВВ ’, однако точка В является также и осью водила Н, которое вращается вокруг О 2. Следовательно, закон распределения линейной скорости по водилу изобразиться прямой линией О 2 В’. Для точки F водила линейная скорость изображается отрезком FF ’.
От вертикали до линии распределения скоростей по водилу измеряем угол ψн, а от вертикали до линии распределения скоростей по колесу 1 измеряем угол ψ1. Т.к. углы ψ1 и ψн отложены от вертикали в одном направлении, то это показывает, что входное звено 1 и выходное звено вращаются в одном направлении.
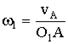
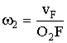
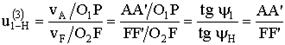 (6.63)
(6.63)
 2015-07-14
2015-07-14 17038
17038








