Результатов наблюдений?

Результат наблюдений, в который введены по­правки с целью устранения систематических погрешностей, считается исправленным. Среднее арифметическое 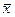из полученных при измерении от­дельных единичных наблюдений вычисляют по формуле:

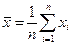, (2.20)

где 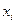— результат наблюдения; п — число единичных наблюдений.

Если во всех результатах содержится постоянная систематиче­ская погрешность, допускается исключать ее после вычисления среднего арифметического неисправленных результатов наблюдений.

Такая запись и подсчет 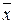удобно лишь при незначительном количестве исходных данных. В случае большого их количества целесообразно использовать другой способ.

Пусть произведено п испытаний, в которых случайная величина Х приняла 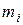раз значение 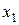, 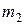раз значение 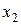, 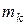раз значение 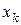, причем 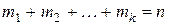. Тогда среднее значение случайной величины 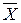определится как среднее арифметическое этих значении:

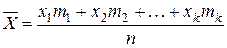(2.27)

или

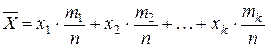(2.28)

Отметим, что отношение 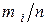есть частость появления значения Х (статистическая вероятность) и, обозначив каждое из них через 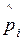, получим

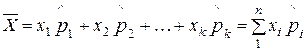(2.29)

Например, пусть 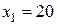, , 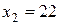, , 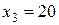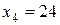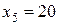. Найти 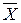. Рассмат-ривая этот ряд величин, заметим, что три из них равны 20, одна — 22, одна — 24. Поэтому частота появления 20 равна 3, 22—1 и частота появления 24—1. Данные сведем в табл. 7.1.

Таким образом,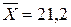

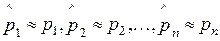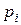При большом числе испытаний , где — значение математической вероятности.

Таблица 2.1

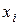
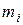
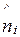
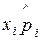
		0,6	12,0
		0,2	4,4
		0,2	4,8
Итого		1,0	21,2

С учетом этого формула (2.29) примет вид

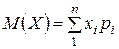(2.30)

Эта формула используется в тех случаях, когда число членов вариационного ряда невелико. В тех случаях, когда используются интервальные ряды, т. е. группируют значения в интервалы, используют формулу

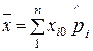(2.31)

где — значение х в середине интервала.

Для облегчения вычислений при большом количестве интервалов удобно использовать метод произведений, приводящий к следующей формуле

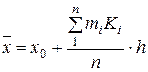(7.32)

где 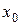— выбранное условное начало, обычно равное значению Х в середине интервала; 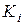— значение, равное разности порядковых номеров между каждым интервалом, т е. 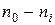; h — ширина интервала.

Таким образом, среднее значение дискретной случайной величины, полученное суммированием произведений всех ее возможных значений на их вероятности, называют математическим ожиданием и обозначают .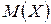

Среднее арифметическое значение 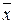будет приближаться к математическому ожиданию 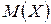с увеличением числа испытаний в серии, т. е. 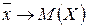, при .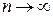

Математическое ожидание – это такая величина, около которой колеблется среднее значение случайной величины, найденное для каждой серии испытаний. В то же время математическое ожидание и среднее значение случайную величину характеризуют не полностью. Рассмотрим пример, в котором дискретные величины Х и Y заданы следующими законами распределения:

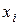
	-0,04	+0,04	Y	-100	+100
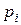
	0,3	0,3		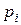0,3	0,3

Математические ожидания этих величин равны:

;

.

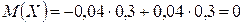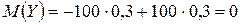Математическое ожидание обеих случайных величин одинаково, а значения величин различны, причем значения 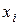были ближе к математическому ожиданию, чем 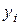. Таким образом, зная лишь математическое ожидание случайной величины, еще нельзя судить о возможных ее значениях и о том, как они отличаются друг от друга и как они группируются (рассеиваются) вокруг своего математического ожидания или среднего значения.

Для более полной характеристики случайной величины используется такая характеристика как дисперсия 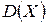, определяющая величину рассеивания случайной величины от ее математического ожидания.