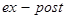2015-07-14
360
(
– прогнозы, 
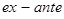– прогнозы)
В формуле (1.11) для определения 1-МНК оценщика регрессанда используются временные ряды наблюдений за Т прошедших периодов, поэтому прогнозные значения полученные по формуле (1.11), являются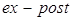 
– прогнозами. Об истинных прогнозах ( 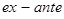– прогнозах) регрессанда говорят тогда, когда во временных рядах прогнозный период лежит после оценочного периода. Качество прогноза будет тем выше, чем:
- полнее выполняются предпосылки модели;
- более надежно (достоверно) оценены параметры модели;
- более точно определены значения регрессоров.
Значение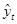 
для будущего периода, вычисленное по формуле
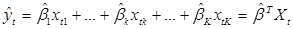(3.1)
может представлять собой:
- оценку математического ожидания регрессанда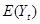 
;
- оценка индивидуального значения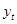 
регрессанда 
.
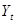При этом предполагается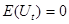 
.
Обозначим ошибку прогноза при оценке математического ожидания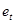 
, а при оценке индивидуального значения регрессанда 
.
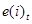Тогда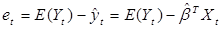 
(3.2)
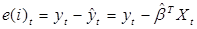(3.3)
И, оцененная дисперсия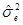 
ошибки прогноза 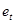и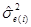 
ошибки прогноза 
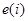равны:
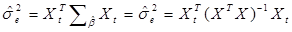(3.4)
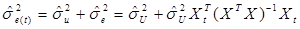(3.5)
Следовательно, оцененная стандартная ошибка для E(Yt) и для индивидуального значения yt равна:
|
|
|
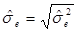или 
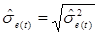(3.6)
Прогнозный интервал (интервальный прогноз, доверительный интервал) величины математического ожидания регрессанда Y при уровне доверия 1–α определяется следующим образом:
– НИЖНЯЯ ГРАНИЦА: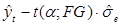 
– ВЕРХНЯЯ ГРАНИЦА: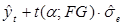 
(3.7)
где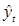 
вычисляется по формуле (2.1); 
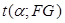берется из таблицы t-критерия (см. приложение) при уровне значимости α и числа степеней свободы 
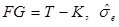вычисляется по формуле (3.6).
При интерпретации данного прогнозного интервала следует различать прогнозный интервал для случайной переменной и для ее реализации. В первом случае он накрывает (включает) математическое ожидание E(Yt) с вероятностью 1–α; во втором случае интервал может включать или не включать E(Yt). Если при этом взять большое число выборок и для каждой из них вычислить соответствующий прогнозный интервал, то эти интервалы накроют E(Yt) с вероятностью (1–α)*100%.
Прогнозный интервал индивидуального значения регрессанда 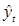вычисляется по формуле (3.7), но вместо величины 
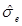используется 
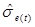. При интерпретации также необходимо заменить E(Yt) на индивидуальное значение .
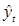ковариационная матрица в этом случае имеет вид:
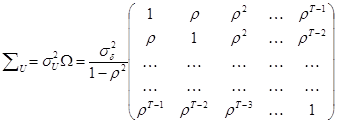[5.7]
Все элементы матрицы Ώ определяются через авторегрессионый параметр ρ, однако при эмпирических исследованиях ρ неизвестно и должно быть статистически оценено.
араметры ц и о, входящие в выражение (11), совпадают с генеральным средним и генеральным среднеквадратическим отклонением случайной величины X. Следовательно, параметр ц определяет положение
