Тема № 4. Многофакторная эконометрическая модель

Как известно, все явления складываются под воздействием не одного, а нескольких факторов. Между факторами существуют сложные взаимосвязи, поэтому их влияние комплексное и его нельзя рассматривать как простую сумму изолированных влияний. В этом случае используют многофакторную економетрическую модель. Ее анализ удобно проводить используя элементы матричной алгебры. При этом объект исследования представляют регрессионной функцией:

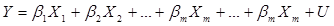, (4.1)

где Y – регрессанд, X₁, X₂, …, X_m – регрессоры, U – случайные переменные.

Для реализации случайных переменных Y_t и U_t уравнение (4.1) примет вид:

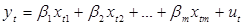(4.2)

Чтобы статистически оценить параметры регрессионной модели, необходимы ряды данных длиной п для регрессандов (Y) и для каждого из К регрессоров (переменных Х). При этом длина рядов наблюдений должна быть больше количества регрессоров (п>m). Длина временных рядов образует опорный (базовый) период. Для наблюдаемых в моменты времени t =1, 2, …, п значений можно записать п уравнений регрессии:

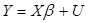, (4.3)

где

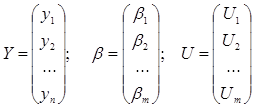(4.4)

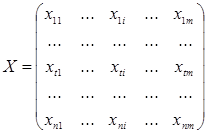
Вектор наблюдений Y и матрица наблюдений Х образуют матрицу данных D.

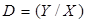(4.5)

Она содержит все данные, необходимые для статистической оценки вектора коэффициентов регрессии 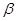и прочих параметров модели.

Метод оценки регрессионных коэффициентов β_m, в котором применяется сумма квадратов ошибок как мера качества адаптации эмпирической функции к наблюдаемым данным, называется одношаговым методом наименьших квадратов (1-МНК). Ошибка уравнения для t-го наблюдения равна:

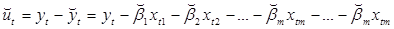(4.6)

Тогда сумма квадратов ошибок 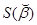для Т наблюдений имеет вид:

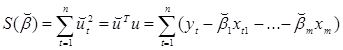(4.7)

или

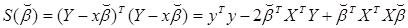
Дифференцируя по 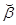, получим, с учетом необходимого условия существования минимума ():

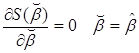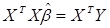, (4.8)

где 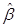- вектор коэффициентов регрессии минимизирующий 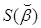; выражение (4.8) называется системой нормальных уравнений. Домножив слева равенство (4.8) на обратную матрицу 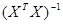, получим формулу для вычисления вектора 1-МНК оценок 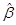для :

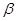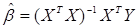(4.9)

Порядок расчетов по формуле (4.9) может быть следующим:

1. Вычислить ;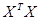

2. Определить вектор ;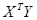

3. Найти матрицу 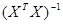обратную матрице ;

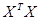4. Рассчитать 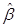как результат произведения 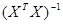на .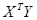

Подставив 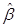в оцениваемое уравнение, получим оцененную с помощью 1-МНК эмпирическую регрессионную функцию:

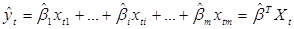(4.10)

Эмпирический коэффициент β_i определяет количество единиц, на которое изменится 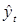при изменении X_i на единицу при прочих равных условиях.

Все n значений 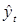– прогноз величины Y (величины ее математического ожидания) образуют вектор Ŷ:

Ŷ 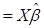(4.11)

Тогда 1-МНК оценщик 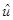вектора возмущений u имеет вид:

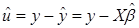(4.12)

Важной характеристикой регрессионной модели является дисперсия возмущений 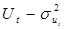. Ее величина должна быть как можно меньше. 1-МНК оценщик для 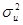можно вычислить по одной из формул:

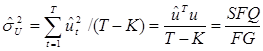(4.13)

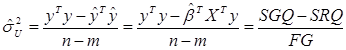(4.14)

где 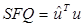- сумма квадратов ошибок; 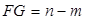- количество степеней свободы; 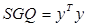- сумма общих квадратов.

Для t – тестирования гипотез по отдельным коэффициентам регрессии и их линейным комбинациям необходимо знать элементы ковариационной матрицы. Ковариационная матрица для 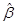, оцененная методом 1-МНК, может быть представлена следующим образом:

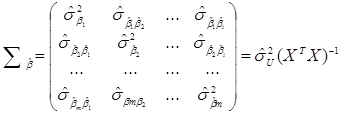(4.15)

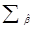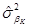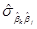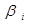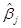На главной диагонали оцененной ковариационной матрицы , i-ый элемент является 1-МНК оценщиком дисперсии i-го коэффициента β_i, а элемент , расположенный вне диагонали, является 1-МНК оценщиком ковариации между и . Наиболее желательными являются, по возможности, узкие доверительные и прогнозные интервалы. И, как следствие, меньшие оцененные дисперсии и ковариации.

Средние коэффициенты эластичности,для линейной регрессии, расчитыва-

ютсяпо формуле:

Э y_xj = а_j x_j / y (4.16)

Для измерения тесноты связи между двумя из рассматриваемых переменных

(без учета их взаимодействия с другими переменными) применяются парные коэффициенты корреляции:

r _{y x1} = (x₁y –x₁ y) /σ _x1 σ_y; r _{y x2} = (x₂y – x₂ y) /σ _x2 σ_y;

r _{x1 x2} = (x₁ x₂ – x₁ x₂) /σ _x1 σ _x2 . (4.17)

где

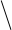
σ _x1 = x₁ ² - (x₁)²

σ _x2 = x₂ ² – (x₂) ²

σ_y = y ² – (y)²

Так как в реальных условиях все переменные, как правило,взаимосвязаны, то на значение коэффициента корреляции частично влияют другие переменные.В связи с этим возникает необходимость исследовать частную корреляцию между переменными при исключении (элиминировании) влияния одной или нескольких переменных. Теснота этой связи определяется частными коэффициентами корреляции.между переменными Xi и Xj при фиксированных значениях остальных m - 2 переменных по формуле:

r _{xixj (x 1,x 2, …, x m)} = - Аij / A ii * Ajj,

где A ii и Ajj -алгебраические дополнения элементов r_ii и r_jj матрицы парных коэффициентов корреляции ∆ r ₁₁ или по рекуррентной формуле:

r _{xixj (x 1,x 2,…,x i-1,x i+1, …, x j-1, x j+1, …,x m)} =

r_{xixj, x 1,x 2,x i-1,x i+1, …, x m -1}-r_{xixm (x 1,x 2, …, x m –1)}r_{xj x m(x 1,x2,…,xm -1)}

(1 –r²_{xixm(x 1,x 2, …, x m –1)}) (1 –r²_{xj x m(x 1,x2,…,xm -1)}) (4.18)

Частные коэффициенты (индексы) корреляции, измеряющие степень и влияние на у фактора хi при неизменом уровне других факторов, можно определить по рекуррентной формуле:

r _{yxi (x 1,x 2,x i-1,x i+1, …, x m)} =

r_{yxi,x1,x2,x i-1,x i+1,…, xm -1}-r_{yxm (x 1,x 2, …, x m –1)}r_{xi x m(x1,x2,…,xm-1)}

(1 –r²_{yxm(x 1,x 2, …, x m –1)}) (1 –r²_{xi x m(x 1,x2,…,xm -1)})

В зависимости от количества переменных, влияние которых исключается, частные коэффициенты корреляции могут быть различного порядка: при исключе-

нии влияния одной переменной получим частный коэффициент корреляции первого порядка; при исключении влияния двух переменных - частный коэф-

фициент корреляции второго порядка и т. д.

Для двухфакторной модели частный коэффициент корреляции первого порядка между признаками х₁ и у при исключении признака х₂ вычисляют по формуле:

r_{y x 1} - r_{yx 2} r_{x 1x2}

r _{yx1 (x 2)} = _______________________

(1 – r²_{yx 2}) (1 – r²_x1x2)

Для двухфакторной модели частный коэффициент корреляциипервого порядка между признаками х₂ и у при исключении признака х₁ вычисляют по формуле:

r_{y x 2} - r_{yx 1} r_{x 1x2}

r _{yx2 (x 1)} = ________________________

(1 – r²_{yx 1}) (1 – r²_x1x2)

Для двухфакторной модели частный коэффициент корреляции первого порядка между признаками х₁ и х₂ при исключении влияния результативного признака у вычисляют по формуле:

r_{х1 x 2} - r_{yx 1} r_уx

r _{х2x1 (у)} = _______________________

(1 – r²_{yx 1}) (1 – r²_уx2),

где r_yxi – парные коэффициенты корреляции между соответствующими признаками.Очевидно, что коэффициент корреляции r между остатками будет отражать тесноту частной корреляции между переменными х_i и х_j при исключении влияния остальных переменных. Можно показать, что коэффициент корреляции r между остатками равен частному коэффициенту корреляции r_xixj. Частный коэффициент корреляции, как и парный коэффициент rij, может принимать значения от –1 до 1 и его значимость оценивают так же, как и обычного коэффициента корреляции r, но при этом полагают df = n – m –2.

Изучение парных и частных коэффициентов корреляции позволяет отобрать наиболее существенные, значимые факторы. Тесноту совместного влияния фак

торов на результат оценивает коэффициент (индекс)множественной корреля-

ции R yx₁x₂,…,x_m:

R yx₁x₂,…,x_m = 1-σ²_{y ост.} /σ²_y

Значение коэффициента (индекса) множественной корреляции лежит в пределах от 0 до 1 и должно быть больше или равно максимальному парному индексу корреляции r _yxi.

В случае линейной двухфакторной связи совокупный коэффициент множественной корреляции можно найти следующим образом:

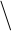R _yx1x2 = (r²_{y x1}+ r²_{y x2} – 2 r _{y x1} r_{y x2} r_{x1 x2} ) / (1 – r²_{x1 x2})

Индекс множественной корреляции для уравнения в стандартизованном виде можно записать следующим образом:

R yx₁x₂,…,x_m = Σ βι r_yxι

При линейной зависимости коэффициент множественной корреляции можно, также, определить через матрицу парных коэффициентов корреляции:

R yx₁x₂,…,x_m = 1- ∆ґ /∆ґ₁₁,

где

1 r_{y x1} r_{y x2} … r_{y x m}

∆ r = r_{y x1} 1 r_x1x2 … r_{x1 x m}

r_{y x 2} r_x2x1 1 … r_{x2 x m}

_{--------------------------------------------------------}

r_{y x m} r_{xm x1} r_{xm x2} … 1

- определитель матрицы парных коэффициентов корреляции;

1 r_{x1 x2} r_x1x3 … r_{x1x m}

∆ r ₁₁ = r_{x2 x1} 1 r_x2x3 … r_{x2 x m}

r_{x3 x 1} r_x3x2 1 … r_{x3 x m}

_{--------------------------------------------------------}

r_{x m x1} r_{xm x2} r_{xm x3} … 1

- определитель матрицы межфакторной корреляции.

Регрессионное уравнение оценено тем лучше, чем больше при прочих равных условиях R².При вычислении R² наблюдается следующая тенденция:R² (c m+1 регрессорами) > R² (c m регрессорами).Следовательно, уравнение с относительно большим числом регрессоров, как правило, будут давать лучшие результаты, чем с малым их количеством. Однако с каждым дополнительным регрессором теряется одна степень свободы, поэтому в статистическом отношении наличие дополнительного регрессора может быть не всегда желательным. Для того, чтобы определить на
какую величину уменьшается R² если i-й регрессор будет исключен, используют частный коэффициент детерминации .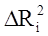

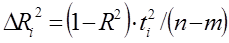[2.5]

где ti- t – статистика для i-го коэффициента. Используя скорректированные коэффициенты детерминации можно определить изменение R², вызванное дополнительным регрессором. Наиболее часто используются скорректированные коэффициенты по Тэйлу:

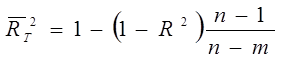[2.6]

и по Амемии:

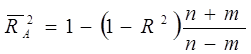[2.7]

Совокупный коэффициент (индекс) множественной детерминации опреде

ляет только качество выравнивания по уравнению регрессии. Так как многофакторный регрессионный анализ оперирует случайными наблюдениями, и необязательно распределенными по многомерному нормальному закону (этому закону должны подчиняться отклонения фактических значений регрессанда от расчетных), то показатели множественной регрессии и корреляции сами могут оказаться подверженными действию случайных факторов. Поэтому только после проверки адекватности уравнения в целом, оно может использоваться для дальнейшего экономического анализа.

Общая оценка адекватности уравнения может быть получена с помощью дисперсионного F – критерия Фишера:

F = R²(n-m-1) / (1- R²). m, или F = σ ²_у .(n-m-1) / σ ²_ост.. m

где m -число факторов.(число параметров р = m + 1)

Полученное значение F– критерия (F_расч.) сравнивают с табличным для принятого уровня значимости и чисел степеней свободы k₁ = m и k₂ = n-m-1.

Если F_расч. > F_{табл .}, то уравнение регрессии статистически значимо, т.е.

доля вариации, обусловленная регрессией, намного превышает случайную ошибку.

Принято считать, что уравнение регрессии пригодно для практического использования в том случае, если F_расч. > F_табл не менее чем в 4 раза.

Частный F – критерий Фишера оценивает статистическую значимость присутствия каждого из факторов в уравнении регрессии и определяется по формуле:

R² yx₁x₂,…,x_m -r ²_{yxi (x 1,x 2,x i-1,x i+1, …, x m)}. (n-m-1)

F_{i част.} =-------------------------------------------------------------------------,

R² yx₁x₂,…,x_m

Или

F_i = 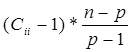, где

С_ii -i –ый диагональный элемент матрицы С обратной к корреляционной матрице R:

C = R^-1, где R = (X^T.X)/(n –1)

Для оценки значимости коэффициентов регрессии при линейной зависимости используют t - критерий Стьюдента при n – (m + 1) степенях свободы:

t_a1 = a₁σ_x1 * √1-r²_x1x2 * √n-m-1 / σ_y √1-R²yx₁x₂

t_a2= a₂σ_x2 * √1-r²_x1x2 * √n-m-1 / σ_y√1-R²yx₁x₂

t_Ryx1x2 = Ryx₁x₂ * √n-m-1 / √1-R²yx₁x₂

Если в уравнении все коэффициенты регрессии значимы, то данное урав -

нение признают окончательным и применяют в качестве модели изучаемого показателя для последующего анализа.

Оценку значимости коеффициентов регрессии с помощью t – критерия

используют, также, для отбора существенных (информативных) факторов при многошаговом регрессионном анализе. Он заключается в том, что после оценки значимости всех коэффициентов регрессии из модели исключают тот фактор, коэффициент при котором незначим и имеет наименьшее значение критерия. Затем строится уравнение регрессии без исключенного фактора, и снова проводится оценка адекватности уравнения и значимости коэфициентов регрессии. Процесс длится до тех пор, пока все коэффициенты регрессии не окажутся значимыми, что свидетельствует о наличии в регрессионной модели только существенных факторов.В некоторых случаях расчетное значение t _расч. находится вблизи t_табл., поэтому с точки зрения содержательности модели такой фактор можно оставить для последующей проверки его значимости в сочетании с другим набором факторов.

При построении уравнения множественной регрессии может возникнуть проблемма мультиколлинеарности факторов, их тесной линейной связи.

Наиболее полно исследовать мультиколлинеарность можно с помощью алгоритма ФАРРАРА-ГЛОБЕРА.Он содержит три вида статистических критериев с помощью которых проверяется мультиколлинеарность соответственно: 1 ). всего массива объясняющих переменных (хи-квадрат);2). каждой объясняющей переменной с остальными объясняющими переменными (F- критерий); 3).каждой пары объясняющих переменных (t -критерий).

АЛГОРИТМ ФАРРАРА –ГЛОБЕРА состоит из следующих шагов:

ШАГ 1. НОРМАЛИЗОВАТЬ ПЕРЕМЕННЫЕ ИСПОЛЬЗУЯ ФОРМУЛУ:

Х* = (Х – Х)/ σк

ШАГ 2. НАЙТИ КОРРЕЛЯЦИОННУЮ МАТРИЦУ R:

R = X* ′ ● X*

ШАГ 3. ОПРЕДЕЛИТЬ КРИТЕРИЙ χ² = - [ n – 1 – 1/6(2m+5)] · ln |R|,

ГДЕ |R| -ОПРЕДЕЛИТЕЛЬ КОРРЕЛЯЦИОННОЙ МАТРИЦЫ.

ЗНАЧЕНИЕ ЭТОГО КРИТЕРИЯ СРАВНИВАЕТСЯ С χ² табл. ПРИ ½(р-1)(р-2) СТЕПЕНИ СВОБОДЫ И УРОВНЮ ЗНАЧИМОСТИ α. ЕСЛИ χ²факт.<χ²табл., ТО В МАССИВЕ НЕЗАВИСИМЫХ ПЕРЕМЕННЫХ М УЛЬТИКОЛЛИНЕАРНО

СТЬ ОТСУТСТВУЕТ.

ШАГ 4. ОПРЕДЕЛИТЬ МАТРИЦУ С ОБРАТНУЮ К R.

C = R ¯ ¹ = (X*´X*)¯ ¹

ШАГ 5. РАССЧИТАТЬ F -КРИТЕРИИ:

Fk = (Ckk - 1) ((n - р) / (р- 1)),

ГДЕ Ckk – ДИАГОНАЛЬНЫЕ ЭЛЕМЕНТЫ МАТРИЦЫ С.

ФАКТИЧЕСКИЕ ЗНАЧЕНИЯ КРИТЕРИЕВ Fk СРАВНИВАЮТСЯ С ТАБЛИЧНЫМИ ПРИ р-1 И n-р СТЕПЕНЕЙ СВОБОДЫ И УРОВНЮ ЗНАЧИМОСТИ α.

ЕСЛИ Fk факт. > Fтабл., ТО СООТВЕТСТВУЮЩАЯ k-Я ОБЪЯСНЯЮЩАЯ ПЕРЕМЕННАЯ МУЛЬТИКОЛЛИНЕАРНА С ДРУГИМИ.

КОЭФФИЦИЕНТ ДЕТЕРМИНАЦИИ ДЛЯ k–ОЙ ПЕРЕМЕННОЙ ВЫЧИСЛЯЕТСЯ ПО ФОРМУЛЕ:

R²k = 1 – 1/Сkk.

ШАГ 6. НАЙТИ ЧАСТНЫЕ КОЭФФИЦИЕНТЫ КОРРЕЛЯЦИИ:

rki = - Скj / √ Скк· Cjj,

ГДЕ Скj -ЭЛЕМЕНТ МАТРИЦЫ С РАСПОЛОЖЕННЫЙ В к – ОЙ СТРОКЕ И j –ОМ СТОЛБЦЕ, Скк И С jj – ДИАГОНАЛЬНЫЕ ЭЛЕМЕНТЫ МАТРИЦЫ С.

ШАГ 7. РАССЧИТАТЬ t – КРИТЕРИИ:

t_kj = (r_ki *√ n – р)/√1-r²_ki.

ФАКТИЧЕСКИЕ ЗНАЧЕНИЯ tkj СРАВНИВАЮТСЯ С ТАБЛИЧНЫМИ ПРИ n-р СТЕПЕНЕЙ СВОБОДЫ И УРОВНЕ ЗНАЧИМОСТИ α.ЕСЛИ tkj факт. > t табл., ТО МЕЖДУ ПЕРЕМЕННЫМИ Хк И Хj СУЩЕСТВУЕТ МУЛЬТИКОЛЛИНЕАРНОСТЬ.

Для устранения или уменьшения мультиколлинеарности используется ряд методов.Самый простой из них состоит в том, что из двух объясняющих переменных, имеющих высокий коэффициент корреляции(больше 0,8),

одну из переменных исключают из рассмотрения.При этом, какую переменную оставить,а какую удалить из анализа, решают в первую очередь на основании экономических соображений.Если с экономической точки зрения ни одной из переменных нельзя отдать предпочтение, то оставляют ту из двух переменных, которая имеет больший коэффициент корреляции с зависимой переменной.

Другой метод устранения или уменьшения мультиколлинеарности заключается в переходе от несмещенных оценок, определяемых по методу 1-МНК, к смещенным оценкам, обладающим, однако, меньшим рассеянием относительно оцениваемого параметра.Так, например, при использовании “ридж-регрессии” или “ гребневой регрессии “вместо несмещенных оценок рассматривают смещенные оценки задаваемые вектором

β=(Х^тХ+τE_p+1)¯¹ X ^т У,

где τ – некоторое положительное число, называемое “ гребнем “ или “ хребтом “, E_p+1- единичная матрица p+1 – го порядка.Добавление τ к диагональным элементам матрицы Х^тХ делает оценки параметров модели смещенными, но при этом увеличивается определитель матрицы системы нормальных уравнений.Вместо Х^тХ он будет равен Х^тХ+τE_{p+ 1} Таким образом, становится возможным исключение мультиколлинеарности в случае, когда определитель Х^тХ близок к нулю.

Возможен, также, переход к новым переменным, представляющим линейные комбинации исходных.В качестве таких переменных берут, например главные компоненты вектора исходных объясняющих переменных и рассматривают регрессию на главных компонентах.

Еще одним из возможных методов устранения или уменьшения мультиколлинеарности является использование пошаговых процедур отбора наиболее информативных переменных.Например,на первом шаге рассматривается лишь одна переменная, имеющая с переменной У наибольший коэффициент детерминации.На втором шаге включается в регрессию новая переменная, которая вместе с первоначально отобранной образует пару переменных, имеющую с У наиболее высокий (скорректированный) коэффициент детерминации, и т. д. Процедура введения новых переменных продолжается до тех пор, пока будет увеличиваться соответствующий (скорректированный) коэффициент корреляции.

На основе коэффициентов регрессии невозможно указать какой из фактор-ных признаков оказывает наибольшее влияние на результативный признак у, так как они не сопоставимы между собой, поскольку измеряются разными единицами.На их основе невозможно также установить в развитии каких фак-

торных признаков заложены наиболее крупные резервы изменения регрессан

да у, потому что в них не учтена вариация факторных признаков.

Для ответа на выше перечисленные вопросы построим уравнение множественной регрессии в стандартизированном виде:

t_y = β_ıt_{x ı} + β₂t _{x 2} + … + β_pt_{x p}

где

t_y = у – у /σ_у, t_хi = (x_i – x_i) /σ_xi - стандартизованные переменные, β_i –

стандартизованные коэффициенты.

Стандартизованные коэффициенты регрессии (β - коэффициенты) опре-

деляются из следующей системы:

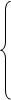β₁ + β₂ r_x1x2 + β₃ r_x1x3 + … + β_p r_x1xp = r_yx1

β₁ r_x2x1 + β₂ + β₃ r_x2x3 + … + β_pr_x2xp = r_yx2

…………………………………………………..

β₁ r_xpx1 + β₂ r_xpx2 +β₃ r_xpx3 + … + β_p = r_yxp

и показывают на какую часть среднего квадратичного отклонения изменяется регрессанд у (результативный признак у) с изменением соответствующего факторного признака на величину его среднего квадратичного отклонения. С помощью β – коэффициентов определяют факторы в развитии которых заложены наиболее крупные резервы изучаемого показателя.

Так как связь коэффициентов множественной регрессии a_i со стандартными коэффициентами β_i (β – коэффициентами) описывается соотношениями:

a_i = β_iσ_у / σ_xi;a₀ = y - b₁ x₁ - b₂ x₂ - … - b_p x_p,

то β - коэффициенты можно также найти по формулам:

β_i = a_i σ_xi/ σ_у,

Средние коэффициенты эластичности для линейной регрессии расчитываются по формуле:

Э y_xj = а_j x_j /y

Частные коэффициенты эластичности вычисляются по формуле:

Э y_xj = а_j x_j /ŷ_{xi (x1,x2,xi-1, xi+1,…,xm)}

и показывают на сколько процентов в среднем изменяется анализируемый показатель с изменением на 1% сответствующего фактора при фиксированном положении других факторов.

С помощью частных коэффициентов эластичности можно определить фак-

тор оказывающий наибольшее влияние на регрессанд у (без учета различия в степени варьирования входящих в уравнение факторов, что, в отличие от β – коэффициентов не дает возможности определить факторы в развитии которых заложены наиболее крупные резервы улучшения изучаемого показателя).

Для определения доли вклада анализируемого фактора в суммарное влияние всех факторов вычисляют∆і - коэффициентпо формуле:

∆_і = β_іr_і/R²

С помощью ∆і – коэффициентов можно определиться фактор, развитием которого можно обеспечить наибольшую долю прироста регрессанда у.

Таким образом на основании частных коэффициентов эластичности Э y_xj,β_i -, ∆і - коэффициентов можно судить о резервах роста исследуемого показателя у (регрессанда у) которые заложены в том или ином факторе x_i.