Свойства непрерывных функций

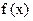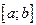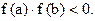Теорема 33.1.(Теорема Больцано-Коши; чеш. математик и философ 1781-1848; франц. математик 1789-1857). Пусть функция определена и непрерывна на отрезке и Тогда существует точка 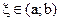такая, что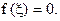

Пример 33.1. Пусть 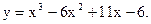Очевидно, что 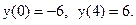Поэтому можно утверждать, что на интервале (0;4) график данной функции хотя бы один раз пересекает ось абсцисс. (В действительности три раза пересекает ось абсцисс при х=1, х=2, х=3, рис. 33.1).

Теорема 33.2. (Теорема Вейерштрасса; нем. математик 1815-1897). Пусть функция 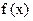определена и непрерывна на отрезке 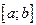. Тогда 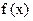ограничена на этом отрезке.

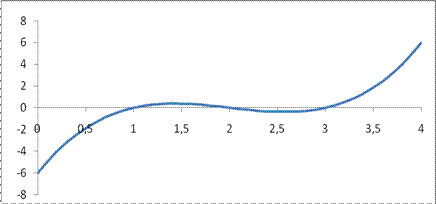Рис. 33.1.

Пример 33.2. На рис. 33.1 дан график функции 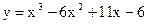. Функция на отрезке [0,4] непрерывна. Значит на интервале (0,4) она не может принимать сколь угодно большие значения.

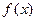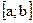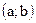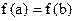Теорема 33.3. (Теорема Ролля; франц. математик 1652-1719). Пусть функция определена и непрерывна на отрезке , дифференцируема в каждой точке интервала и . Тогда существует точка 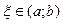такая, что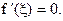

Пример 33.1. На рисунке 33.3 дан график функции

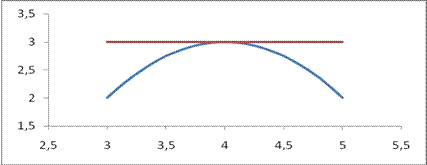
Рис. 33.3.

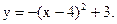Т.К. функция непрерывна на отрезке [3,5], диффуренцируема внутри этого отрезка и 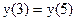. Поэтому внутри отрезка [3,5] найдется по крайней мере одна точка, в которой касательная горизонтальна.