Необходимые условия возрастания (убывания) функции

Теорема. Если функция дифференцируема и возрастает (убывает) на 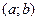, то ()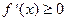

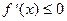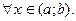
Пример 36.1. Функция, график которой указан на рис.36.1, возрастает на отрезке [-3,-2]. Поэтому тангенс угла наклона касательной (на этой части графика) не может быть отрицательным. При х=-2 тангенс угла наклона касательной равен нулю: 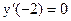(касательная горизонтальная, см. рис. 36.1).

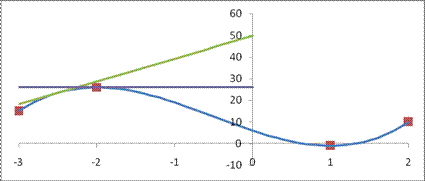
Рис. 36.1.

Достаточные условия возрастания (убывания) функции

Теорема. Если 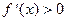(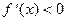) 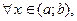то 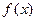возрастает (убывает) на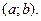

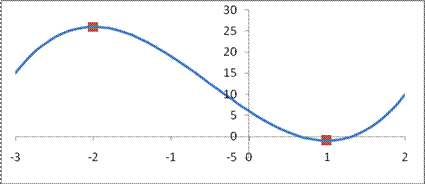
Рис. 37.1.

Пример 37.1. Рассмотрим (см. рис. 37.1) функцию 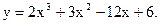Ее производная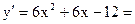

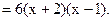Приравняем производную нулю 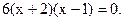Производная равна нулю пр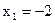и и 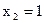(см. рис. 37.1, касательные в этих точках горизонтальные). На рис. 37.2 указаны знаки производной нашей функции. Пользуясь формулой 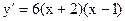замечаем, что производная положительна при 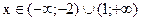и отрицательна при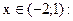

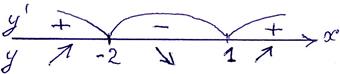
Рис. 37.2.

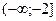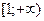Поэтому на промежутках и функция возрастает, а на промежутке 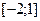- убывает (см. рис. 37.1).