2015-07-14
283
(франц. математик 1736-1813)
Теорема. Пусть функция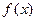 
определена и непрерывна на отрезке 
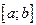и дифференцируема в каждой точке интервала 
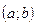. Тогда существует точка 
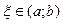такая, что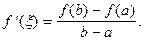 
Пример 34.1. На рис. 34.1 дан график функции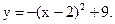 
Рассмотрим участок графика между точками A(0;5) и В(2;9). Т.к. наша функция удовлетворяет условиям теоремы, то теорема Лагранжа утверждает, что на интервале найдется (по крайней мере одна) точка, через которую проведенная касательная параллельна прямой, проходящей через точки А и В.
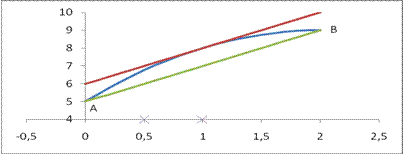
Рис. 34.1.
