Пусть заданы прямая 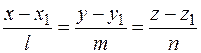 и плоскость
и плоскость 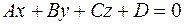 . Угол
. Угол 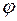 между ними можно найти по формуле
между ними можно найти по формуле
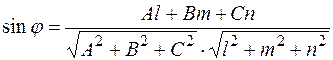 .
.
Задача 73. Написать канонические уравнения прямой
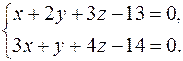 (11)
(11)
Решение. Для того чтобы записать канонические уравнения прямой (9), необходимо знать любую точку, принадлежащую прямой, и направляющий вектор прямой.
Найдём вектор 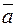 , параллельный данной прямой. Так как он должен быть перпендикулярен к нормальным векторам данных плоскостей, т. е.
, параллельный данной прямой. Так как он должен быть перпендикулярен к нормальным векторам данных плоскостей, т. е.
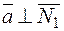 ,
, 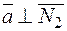 , то
, то
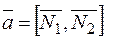 .
.
Из общих уравнений прямой имеем, что 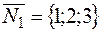 ,
, 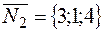 . Тогда
. Тогда
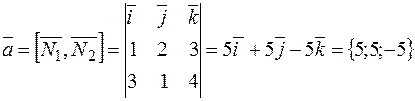 .
.
Так как точка 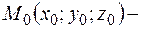 любая точка прямой, то её координаты должны удовлетворять уравнениям прямой и одну из них можно задать, например,
любая точка прямой, то её координаты должны удовлетворять уравнениям прямой и одну из них можно задать, например, 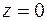 , две другие координаты найдём из системы (11):
, две другие координаты найдём из системы (11):
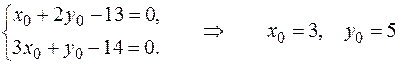 .
.
Отсюда, 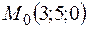 .
.
Таким образом, канонические уравнения искомой прямой имеют вид:
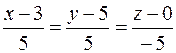 или
или 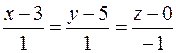 .
.
Задача 74. Вычислить расстояние между параллельными прямыми:
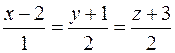 и
и 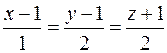 .
.
Решение. Из канонических уравнений первой прямой известны координаты точки 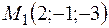 , принадлежащей прямой, и координаты направляющего вектора
, принадлежащей прямой, и координаты направляющего вектора 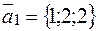 . Из канонических уравнений второй прямой также известны координаты точки
. Из канонических уравнений второй прямой также известны координаты точки 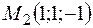 и координаты направляющего вектора
и координаты направляющего вектора 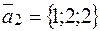 .
.
Расстояние между параллельными прямыми равно расстоянию точки 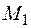 от второй прямой. Это расстояние вычисляется по формуле
от второй прямой. Это расстояние вычисляется по формуле
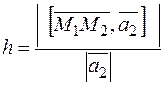 .
.
Найдём координаты вектора 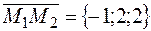 .
.
Вычислим векторное произведение 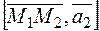 :
:
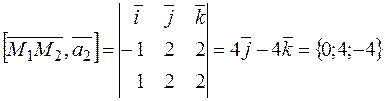 .
.
Тогда
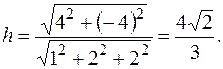
Задача 75. Найти точку 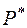 симметричную точке
симметричную точке 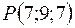 относительно прямой
относительно прямой
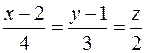 .
.
Решение. Запишем уравнение плоскости перпендикулярной к данной прямой и проходящей через точку 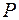 . В качестве её вектора нормали
. В качестве её вектора нормали 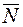 можно взять направляющий вектор прямой. Тогда
можно взять направляющий вектор прямой. Тогда 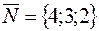 . Следовательно,
. Следовательно,
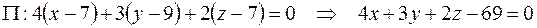 .
.
Найдём точку 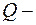 точку пересечения данной прямой и плоскости П. Для этого запишем параметрические уравнения прямой, используя уравнения (10), получим
точку пересечения данной прямой и плоскости П. Для этого запишем параметрические уравнения прямой, используя уравнения (10), получим
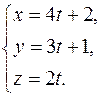
Далее, решим систему, в которую входит уравнение плоскости и параметрические уравнения прямой:
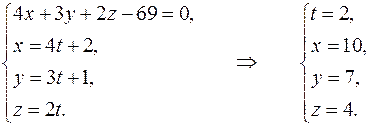
Следовательно, 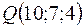 .
.
Пусть 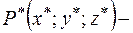 точка симметричная точке
точка симметричная точке 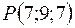 относительно данной прямой. Тогда точка
относительно данной прямой. Тогда точка 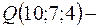 середина отрезка
середина отрезка 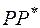 . Для нахождения координат точки
. Для нахождения координат точки 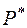 используем формулы координат середины отрезка:
используем формулы координат середины отрезка:
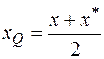 ,
, 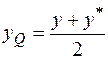 ,
, 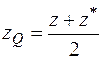 .
.
Получим
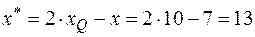 ,
, 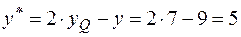 ,
,
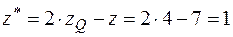 .
.
Итак, 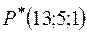 .
.
Задача 76. Написать уравнение плоскости, проходящей через прямую 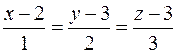 и
и
а) через точку 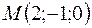 ;
;
б) перпендикулярно плоскости 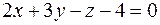 .
.
Решение. Запишем общие уравнения данной прямой. Для этого рассмотрим два равенства:
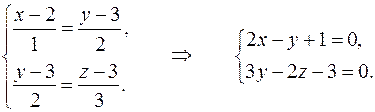
Это означает, что искомая плоскость принадлежит пучку плоскостей с образующими 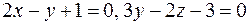 и её уравнение может быть записано в виде (8):
и её уравнение может быть записано в виде (8):
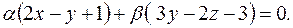 (12)
(12)
а) Найдём 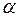 и
и 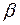 из условия, что плоскость проходит через точку
из условия, что плоскость проходит через точку 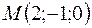 , следовательно, её координаты должны удовлетворять уравнению плоскости. Подставим координаты точки
, следовательно, её координаты должны удовлетворять уравнению плоскости. Подставим координаты точки 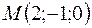 в уравнение пучка плоскостей:
в уравнение пучка плоскостей:
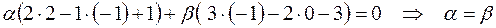 .
.
Найденное значение 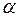 подставим в уравнение (12). получим уравнение искомой плоскости:
подставим в уравнение (12). получим уравнение искомой плоскости:
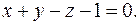
б) Найдём 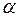 и
и 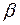 из условия, что искомая плоскость перпендикулярна плоскости
из условия, что искомая плоскость перпендикулярна плоскости 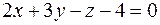 . Вектор нормали данной плоскости
. Вектор нормали данной плоскости 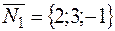 , вектор нормали искомой плоскости
, вектор нормали искомой плоскости 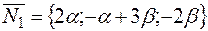 (см. уравнение пучка плоскостей (12).
(см. уравнение пучка плоскостей (12).
Два вектора перпендикулярны тогда и только тогда, когда их скалярное произведение равно нулю. Следовательно,
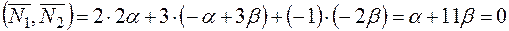 .
.
Отсюда,
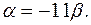
Подставим найденное значение 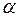 в уравнение пучка плоскостей (12). Получим уравнение искомой плоскости:
в уравнение пучка плоскостей (12). Получим уравнение искомой плоскости:
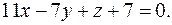
 2015-07-14
2015-07-14 756
756








