Дифференцирование сложных и неявных функций
Пусть задана функция двух переменных:
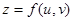
и пусть переменные 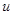 и
и 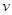 сами являются непрерывными функциями независимых переменных
сами являются непрерывными функциями независимых переменных  и
и 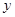 :
:
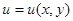 ,
, 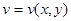 . (*)
. (*)
Таким образом,
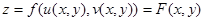 ,
,
т.е. 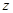 является сложной функцией переменных
является сложной функцией переменных  и
и 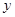 . Выясним, как найти ее частные производные по аргументам
. Выясним, как найти ее частные производные по аргументам  и
и 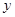 , не делая непосредственной подстановки. При этом будем предполагать, что все рассматриваемые функции имеют непрерывные частные производные по всем своим аргументам.
, не делая непосредственной подстановки. При этом будем предполагать, что все рассматриваемые функции имеют непрерывные частные производные по всем своим аргументам.
Сначала найдем производную 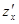 . Для этого дадим аргументу
. Для этого дадим аргументу  приращение
приращение 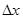 , сохраняя значение
, сохраняя значение 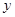 неизменным. Тогда в силу уравнений (*) получат приращения
неизменным. Тогда в силу уравнений (*) получат приращения 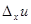 и
и 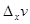 .
.
Но если 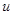 и
и 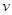 получают приращения
получают приращения 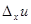 и
и 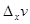 , то функция
, то функция 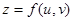 получит приращение
получит приращение 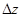 , определяемое формулой (см. §3):
, определяемое формулой (см. §3):
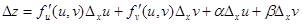 .
.
Разделим обе части последнего равенства на 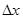 :
:
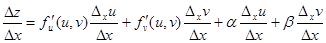 .
.
Если 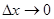 , то
, то 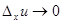 и
и 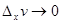 (в силу непрерывности функций
(в силу непрерывности функций 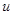 и
и 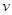 ). Но тогда
). Но тогда 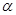 и
и 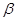 тоже стремятся к нулю. Переходя к пределу при
тоже стремятся к нулю. Переходя к пределу при 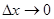 , получим
, получим
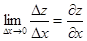 ,
, 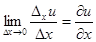 ,
, 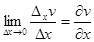 ,
,
и, следовательно,
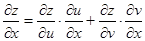 . (1)
. (1)
Аналогично находим производную 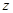 по переменной
по переменной 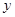 :
:
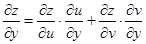 . (2)
. (2)
Вывод. Частная производная сложной функции равна сумме произведений частных производных заданной функции по промежуточным аргументам (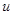 и
и 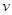 ) на частные производные этих аргументов (
) на частные производные этих аргументов (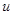 и
и 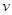 ) по соответствующей независимой переменной (
) по соответствующей независимой переменной ( и
и 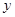 ).
).
Пример 1. Найти частные производные сложной функции 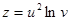 , где
, где 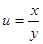 ,
, 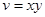 .
.
Решение.
Находим сначала частные производные данных функций:
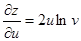 ,
, 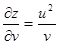 ,
,
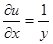 ,
, 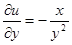 ,
, 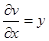 ,
, 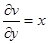 .
.
По формулам (1) и (2) находим производные от сложной функции:
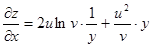 ;
;
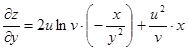
В полученные выражения для производных вместо 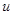 и
и 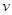 можно подставить их выражения через
можно подставить их выражения через  и
и 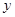 .
.
Тогда окончательно получим:
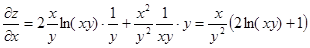 ;
;
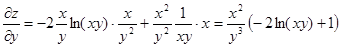 .
.
Частные случаи.
1. Пусть 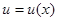 и
и 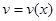 . Тогда функция
. Тогда функция 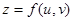 является фактически функцией одной переменной
является фактически функцией одной переменной  , следовательно, можно ставить вопрос о нахождении обычной производной
, следовательно, можно ставить вопрос о нахождении обычной производной 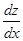 . Эту производную можно найти по формуле (5.1), заменяя в ней частные производные по
. Эту производную можно найти по формуле (5.1), заменяя в ней частные производные по  на обычные.
на обычные.
Таким образом, получим:
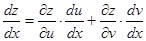 . (3)
. (3)
Пример 2. Найти производную 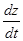 для функции
для функции 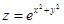 , где
, где 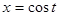 и
и 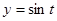 .
.
Решение.
Учитывая, что функция 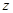 фактически является сложной функцией одной переменной
фактически является сложной функцией одной переменной 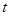 , то для нахождения ее производной по этой переменной необходимо использовать формулу, аналогичную формуле (5.3).
, то для нахождения ее производной по этой переменной необходимо использовать формулу, аналогичную формуле (5.3).
Имеем:
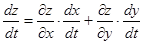 .
.
Теперь найдем все производные, входящие в правую часть полученной формулы:
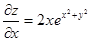 ,
, 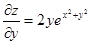 ,
, 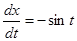 ,
, 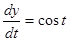 .
.
Следовательно, имеем:
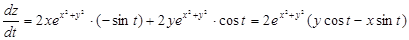 .
.
Выразив  и
и 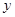 через
через 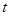 , окончательно получим
, окончательно получим
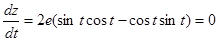 .
.
2. Пусть задана функция 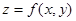 , причем
, причем  является независимой переменной, а
является независимой переменной, а 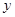 – функцией от
– функцией от  , т.е.
, т.е. 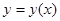 . Следовательно, функция
. Следовательно, функция 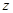 является сложной функцией переменной
является сложной функцией переменной  : эта переменная является ее первым аргументом, а также входит как независимая переменная во второй аргумент
: эта переменная является ее первым аргументом, а также входит как независимая переменная во второй аргумент 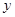 . Тогда согласно формуле (5.3) будем иметь
. Тогда согласно формуле (5.3) будем иметь
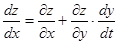 , (4)
, (4)
так как 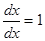 .
.
Эта формула есть формула для вычисления полной производной 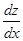 (в отличие от частной производной
(в отличие от частной производной 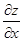 ).
).
Необходимо обратить внимание на различие между двумя производными по  , содержащимися в формуле (4). В то время как
, содержащимися в формуле (4). В то время как 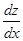 есть полная производная, т.е. обыкновенная производная от
есть полная производная, т.е. обыкновенная производная от 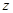 по аргументу
по аргументу  ,
, 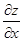 есть частная производная от
есть частная производная от 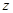 по аргументу
по аргументу  , входящему в выражение функции непосредственно, значит, при условии, что аргумент
, входящему в выражение функции непосредственно, значит, при условии, что аргумент 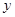 , хотя он и зависит от
, хотя он и зависит от  , при дифференцировании остается постоянным.
, при дифференцировании остается постоянным.
Пример 3. Найти 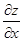 и
и 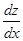 , если
, если 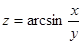 , где
, где 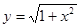 .
.
Решение.
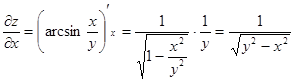 .
.
Полная производная 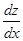 вычисляется по формуле (4):
вычисляется по формуле (4):
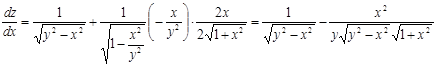 .
.
Поскольку 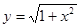 , то
, то 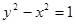 , и окончательно получаем:
, и окончательно получаем:
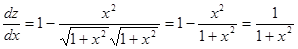 .
.
Замечание 1. Сформулированное выше правило дифференцирования сложной функции остается справедливым для функций любого числа независимых переменных и при всяком числе промежуточных аргументов.
Пусть 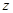 задана как функция аргументов
задана как функция аргументов 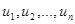 , т.е.
, т.е. 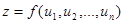 , которые являются функциями независимых переменных
, которые являются функциями независимых переменных 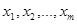 . Тогда
. Тогда
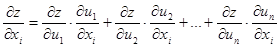 , (5)
, (5)
где 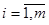 .
.
 2015-07-14
2015-07-14 9424
9424