Пусть дано уравнение
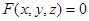 ,
,
связывающее значения трех переменных  ,
, 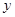 и
и 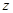 . Рассмотрим множество тех пар чисел
. Рассмотрим множество тех пар чисел 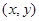 , для которых значения
, для которых значения 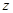 , обращающие совместно с
, обращающие совместно с  ,
, 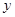 то уравнение в тождество.
то уравнение в тождество.
Подставив каждой паре чисел 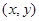 из этого множества в соответствие те значения
из этого множества в соответствие те значения 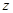 , для которых
, для которых 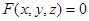 , получим однозначную или многозначную функцию двух переменных
, получим однозначную или многозначную функцию двух переменных
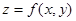 .
.
Функцию 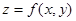 будем называть неявно заданной уравнением
будем называть неявно заданной уравнением 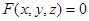 , или просто неявной функцией двух переменных.
, или просто неявной функцией двух переменных.
Найдем частные производные 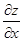 и
и 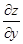 неявной функции
неявной функции 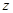 , определяемой уравнением
, определяемой уравнением 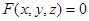 .
.
Когда ищем 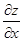 , то считаем аргумент
, то считаем аргумент 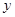 постоянным. Поэтому здесь применима формула (5.6), если только независимой переменной считать
постоянным. Поэтому здесь применима формула (5.6), если только независимой переменной считать  , а функцией
, а функцией 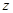 . Следовательно,
. Следовательно,
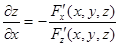 . (7)
. (7)
Аналогично находим производную 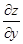 :
:
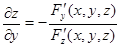 . (8)
. (8)
Обе формулы найдены в предположении, что 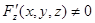 .
.
Пример 5. Найти частные производные функции 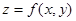 , заданной неявно уравнением
, заданной неявно уравнением 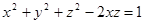 .
.
Решение.
В данном случае 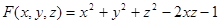 , поэтому имеем
, поэтому имеем
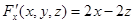 ,
, 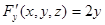 ,
, 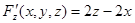 .
.
Следовательно, по формулам (7) и (8) находим
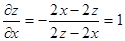 ,
, 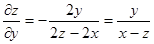 .
.
В общем случае, когда уравнение
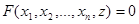
Определяет 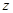 как некоторую функцию от
как некоторую функцию от 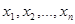 , аналогично предыдущему найдем
, аналогично предыдущему найдем
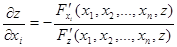 , (9)
, (9)
где 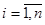 .
.
 2015-07-14
2015-07-14 4433
4433