Пусть гладкая функция 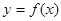 неявно определяется из уравнения
неявно определяется из уравнения
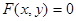 , (**)
, (**)
где 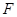 – некоторая функция от двух переменных. Это значит, что если в (**) вместо
– некоторая функция от двух переменных. Это значит, что если в (**) вместо 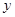 подставить
подставить 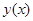 , то получим тождество
, то получим тождество
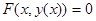 . (***)
. (***)
Для общего уравнения (**) поставим задачу найти производную 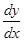 , не разрешая его относительно
, не разрешая его относительно 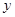 .
.
Предположим, что существуют непрерывные частные производные 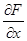 ,
, 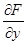 и рассмотрим тождество (***). Левую часть этого тождества можно рассматривать как сложную функцию, зависящую от
и рассмотрим тождество (***). Левую часть этого тождества можно рассматривать как сложную функцию, зависящую от  и непосредственно, и через второй аргумент. Причем из (***) следует, что эта функция тождественно равна нулю. Следовательно, и производная от нее по
и непосредственно, и через второй аргумент. Причем из (***) следует, что эта функция тождественно равна нулю. Следовательно, и производная от нее по  должна быть равна нулю. Находя производную по формуле (4), получим
должна быть равна нулю. Находя производную по формуле (4), получим
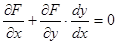 ,
,
откуда, если 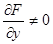 , имеем
, имеем
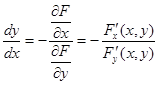 . (6)
. (6)
Пример 4. Найти 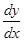 , если функция
, если функция 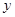 задана неявно уравнением
задана неявно уравнением 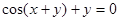 .
.
Решение.
Здесь 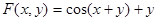 . Найдем частные производные этой функции:
. Найдем частные производные этой функции:
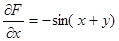 ,
, 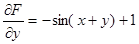 .
.
Следовательно, используя формулу (5.6), получаем:
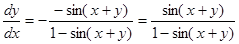 .
.
 2015-07-14
2015-07-14 1645
1645
