2015-07-14
1957
Практическое использование гидродинамических моделей в процессе математического моделирования химико-технологических систем возможно только тогда, когда известны численные значения параметров гидродинамических моделей. К таким параметрам относятся для модели идеального смешения – среднее время пребывания продукта в аппарате Т, для модели идеального вытеснения - время Т, для диффузионной модели – время Т и коэффициент продольного перемешивания DL, для ячеечной модели – время Т и число ячеек смешения m. Эти параметры можно вычислить в ходе обработки экспериментальной функции отклика аппарата на импульсное возмущение при помощи статистических моментов.
В теории вероятности статистические моменты позволяют получать ряд характеристик функций распределения случайной величины. Функцию отклика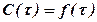 
также можно интерпретировать как функцию распределения случайной величины. Различают начальные и центральные статистические моменты. Начальные статистические моменты рассчитывают по фактической функции распределения (функции отклика 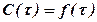), центральные моменты – по функции распределения (функции отклика 
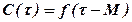) смещенной относительно фактического расположения по оси 
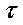на величину математического ожидания среднего времени пребывания потока в аппарате М (рис. 1.24).
|
|
|
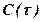
М
 | |||
 |
0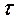 
Рис. 1.24. К расчету начальных и центральных статистических моментов (М - математического ожидание среднего времени пребывания потока в аппарате)
Различают ряд начальных и центральных статистических моментов, отличающихся по порядку моментов, в общем случае статистические моменты S -ого порядка рассчитываются по уравнениям для начальных моментов
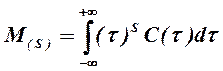, (1.28)
а для центральных моментов
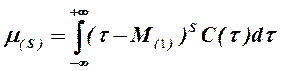, (1.29)
где М(1) – первый начальный статистический момент.
Из всего многообразия статистических моментов с позиций расчета параметров гидродинамических моделей наибольший интерес представляют нулевой и первый начальный моменты и второй центральный момент.
Нулевой начальный статистический момент
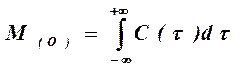(1.30)
характеризует площадь под функцией отклика и эквивалентен (пропорционален в масштабе эксперимента) величине возмущения, например, количеству трассера, проходящего по соответствующей ветви комбинированной гидродинамической модели и, соответственно, количеству технологического потока, проходящего по этой ветви.
