Начальные и центральные моменты случайной величины

Обобщением основных числовых характеристик случайной величины являются понятия моментов. Название заимствовано из механики, где эти понятия применяются для описания распределения масс.

Определение 13. Начальным моментом k-го порядка случайной величины 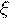называется математическое ожидание случайной величины .

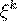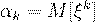(29)

Если 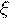- дискретная случайная величина, принимающая конечное число значений, то

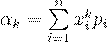(30)

Если 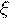- дискретная случайная величина, принимающая бесконечное, но счетное число значений, то

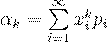(31)

Если 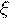- непрерывная случайная величина, принимающая значение на конечном промежутке 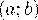, то

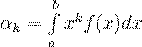(32)

Если 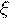- непрерывная случайная величина, принимающая значения на всей числовой оси, то

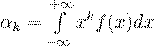(33)

Начальный момент 1-го порядка - это математическое ожидание случайной величины: .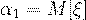
Начальные моменты высших порядков главным образом используются для вычисления центральных моментов.

Определение 14. Центральным моментом k-го порядка случайной величины 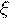называется математическое
ожидание случайной величины .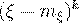

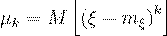(34)

Если случайная величина 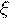- дискретная, принимающая конечное число значений, то

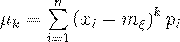(35)

Если случайная величина 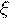- дискретная, принимающая бесконечное, но счетное число значений, то

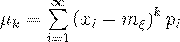(36)

Если случайная величина 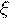- непрерывная, принимающая значения на конечном промежутке 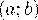, то

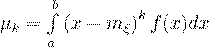(37)

Если случайная величина 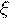- непрерывная, принимающая значения на всей числовой оси, то

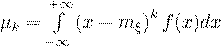(38)

1. Центральный момент 1-го порядка равен нулю: .
2. Центральный момент 2-го порядка - это дисперсия случайной величины: .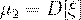
3. Центральный момент 3-го порядка служит характеристикой асимметрии(" скошенности") распределения.
Если распределение случайной величины 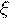- симметричное, то .
Число, которое находится по формуле:

(39)

называется коэффициентом асимметрии.
Если 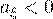, то распределение имеет левостороннюю "скошенность", график плотности распределения имеет вид:

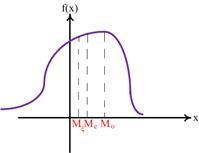
Рис.11

Тогда .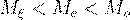

Если 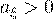, то распределение имеет правостороннюю "скошенность", график плотности распределения в этом
случае имеет вид:

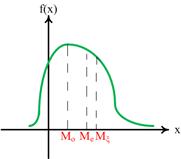
Рис.12

Тогда .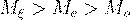

4. Центральный момент 4-го порядка служит характеристикой "островершинности" или "плосковершинности"
распределения. Эти свойства распределения описываются с помощью эксцесса, который вычисляется по формуле:

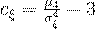(40)

Для наиболее распространенного нормального распределения(подробно о котором будет изложено в лекции
"Законы распределения случайных величин") . Кривая нормального распределения принята за эталон,
остальные с ней сравниваются. Для "островершинных" распределения 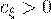, для "плосковершинных"
распределений (см. рис.13):

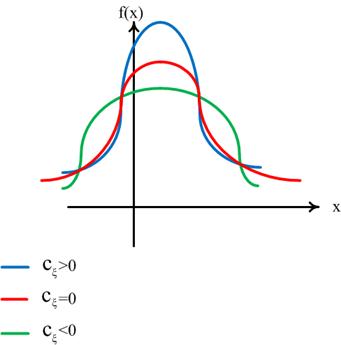
Рис.13

Пример 14. Дискретная случайная величина 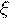задана рядом распределения:

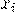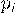	0,4	0,6

Найти центральные моменты 1-го, 2-го и 3-го порядков.

Решение. Сначала найдем начальный момент 1-го порядка, то есть математическое ожидание случайной
величины, получаем:.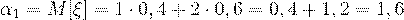
Центральный момент 1-го порядка равен 0.
Центральный момент 2-го порядка - это дисперсия случайной величины, вычисляем ее по формуле (35):
.
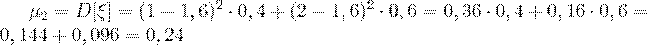Аналогично по формуле (35) вычисляем центральный момент 3-го порядка:
.

Вопрос. Центральный момент 3-го порядка 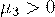, тогда коэффициент асимметрии :
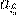а) больше нуля;
б) меньше нуля;
в) равен нулю;
г) невозможно ответить на этот вопрос.

б)

в)

г)

а)