Градиентные методы нелинейного программирования

Из большого числа градиентных методов остановимся на методе двух производных, являющимся одним из наиболее быстродействующих методов нелинейного программирования. В этом методе переход из одной точки сканирования оси Х в другую выполняется с шагами, равными инкременту 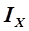, то есть отношению первой и второй производных от целевой функции, без расчета критерия оптимальности на каждом шаге;

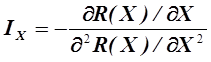. (5.36)

Переход из предыдущей точки 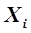в последующую точку 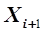выполняется по формуле

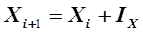. (5.37)

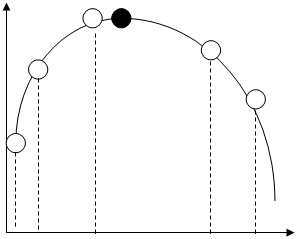
Метод основан на специфических свойствах инкремента. Рассмотрим качественно характер инкремента в при различных значениях параметра Х (рис. 5.5), если заданы целевая функция 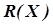= МАХ, область исследования 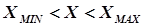и погрешность определения точки экстремума .

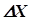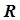
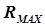
1 2

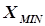Х₁ Х₃Х₂ 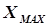Х

Рис. 5.5. Иллюстрация метода двух производных

Анализ первой точки показывает, что при Х=Х₁ производная 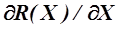является положительной величиной, а вторая производная 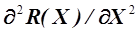– отрицательной, тогда величина инкремента 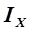является положительной и от точки Х₁ мы переместимся вправо в направлении к экстремуму в новую расчетную точку. Во второй точке при Х=Х₂ производная 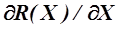является отрицательной величиной, и вторая производная 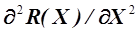– отрицательна, тогда величина инкремента 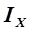станет отрицательной и от точки Х₂ мы переместимся влево в направлении к экстремуму в новую расчетную точку. Сопоставляя поведение расчета в точках 1 и 3, нетрудно заметить, что в обоих случаях инкременты положительны, но будет существенно меньше 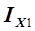, таким образом, чем ближе находится расчетная точка к экстремуму, тем меньше величина очередного шага, при попадании в ходе решения задачи точно в точку экстремума получаем величину 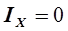. Таким образом метод самостоятельно перемещает точку поиска экстремума в околоэкстремальную область без расчета критерия оптимальности, что существенно ускоряет расчет задачи оптимизации.

Алгоритм решения предельно прост:

1. В области исследования задачи 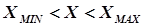выбираем произвольную точку Х и рассчитываем для нее величину инкремента .

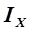2. Переходим в новую точку расчета 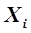с шагом, равным величине инкремента .

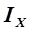3. Расчет по пункту 2 выполняем до тех пор, пока величина 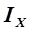не станет меньше погрешности расчета 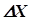и по последнему значению параметра Х рассчитывается значение критерия оптимальности .

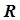Особенности поиска оптимальных условий ведения процесса