Правила дифференцирования

(C)’= 0 С=const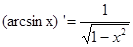
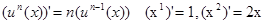
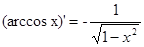
(cos x)'=-sin x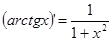
(sin x)'=cos x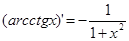
(tg x)'=	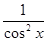(ах)'=аx ln a
(ctg x)'=-	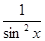(ех)'=ex

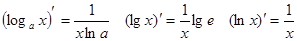
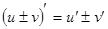
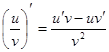
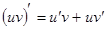
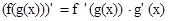
Производная степенно-показательной функции

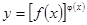, где .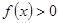

.

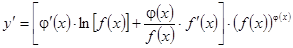Логарифмическое дифференцирование. Пусть дана функция 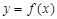. При этом предполагается, что функция 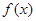не обращается в нуль в точке 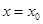. Покажем один из способов нахождения производной функции , если 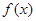очень сложная функция и по обычным правилам диф­фе­рен­цирования найти производную затруднительно.

Так как по первоначальному предположению 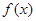не равна нулю в точке, где ищется ее производная, то найдем новую функцию 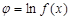и вычислим ее производную

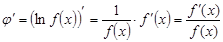(1)

Отношение 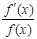называется логарифмической производной функции 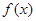. Из формулы (1) получаем

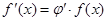. Или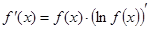

Формула (2) дает простой способ нахождения производной функции .