Достаточные условия экстремума

Теорема 3. Пусть функция f(x) непрерывна в некоторой окрестности точки х₀, дифференцируема в проколотой окрестности этой точки и с каждой стороны от данной точки f ‘(x) сохраняет постоянный знак. Тогда:

1) если f ‘(x) > 0 при x < x₀ и f ‘(x) < 0 при x > x₀, точка х₀ является точкой максимума;

2) если f ‘(x) < 0 при x < x₀ и f ‘(x) > 0 при x > x₀, точка х₀ является точкой минимума;

3) если f ‘(x) не меняет знак в точке х₀, эта точка не является точкой экстремума.

Доказательство.

Справедливость утверждения 3) следует из теоремы 1. Докажем утверждения 1) и 2). По формуле Лагранжа f(x) – f(x₀) = f ‘(x)(x – x₀), где х принадлежит окрестности точки х₀, а x лежит между х и х₀. Если f ‘(x) > 0 при x < x < x₀ и f ‘(x) < 0 при х₀ < x < x, приращение функции f(x) – f(x₀) < 0 по обе стороны х₀, то есть в рассматриваемой точке достигается максимум. Если же производная при х = х₀ меняет знак с «+» на «-», точка х₀ является точкой минимума. Следовательно, изменение знака производной в точке х₀ является необходимым и достаточным условием наличия экстремума в этой точке.

Теорема 4. Пусть f ‘(x₀) = 0 и у рассматриваемой функции существует непрерывная вторая производная в некоторой окрестности точки х₀. Тогда х₀ является точкой максимума, если f’’(x₀) < 0, или точкой минимума, если f’’(x₀) > 0.

Доказательство.

Докажем первую часть теоремы. Пусть f’’(x₀) < 0. Так как по условию f’’(x) непрерывна, существует окрестность точки х₀, в которой f’’(x) < 0. Вспомним, что f’’(x) = (f ’(x))’, и из условия (f’(x))’ < 0 следует, что f'(x) убывает в рассматриваемой окрестности. Поскольку f’(x₀) = 0, f’(x) > 0 при x < x₀ и f’(x) > 0 при x > x₀. Тогда по теореме 3 точка х₀ является точкой максимума функции, что и требовалось доказать. Утверждение 2) доказывается аналогично.

Теорема 5. Пусть функция y = f(x) n раз дифференцируема в точке х₀ и f ^(k)(x₀) = 0 при k = 1,2,…, n -1, а f ⁽ⁿ⁾ (x₀) не равна нулю. Тогда, если n – четное число (n = 2 m), функция f(x) имеет в точке х₀ экстремум, а именно максимум при f ^(2m)(x₀) < 0 и минимум при f ^{( 2 m)}(x₀) > 0. Если же n – нечетное число (n = 2 m – 1), то точка х₀ не является точкой экстремума.

Доказательство.

Из формулы Тейлора следует, что

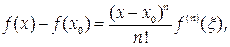
где x лежит между х и х₀.

а) Если n = 2 m – четное и f ^(2m)(x₀) < 0, то найдется окрестность точки х₀, в которой f ^(2m) (x) < 0. Пусть х принадлежит этой окрестности, тогда x тоже ей принадлежит, то есть f ^(2m)(x) < 0. Но (x – x₀)^2m > 0 при х, не равном х₀, поэтому f(x) – f(x₀) < 0 во всей рассматриваемой окрестности, следовательно, точка х₀ является точкой максимума.

б) Если n = 2 m – четное и f ^(2m)(x₀) > 0, то таким же образом доказывается, что х₀ – точка минимума.

в) Если n = 2 m - 1 – нечетное, то (x – x₀) ^{2 m- 1} имеет разные знаки по разные стороны точки х₀. Поэтому в окрестности этой точки, в которой производная порядка 2 m – 1 сохраняет постоянный знак, приращение функции меняет знак при х = х₀. Следовательно, экстремум в этой точке не достигается.

Вывод: проверить наличие экстремума в критической точке можно тремя способами:

1) убедиться, что f’(x) меняет знак при х = х₀;

2) определить знак f’’(x₀);

3) если f’’(x₀) = 0, исследовать порядок и знак производной, не обращающейся в 0 в рассматриваемой точке.