Решение

Область определения функции: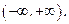

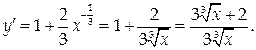
Функция имеет две критические точки:

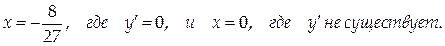
Исследуем знак производной на интервалах, разделенных критическими точками:

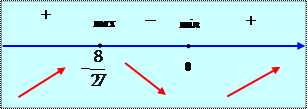
Рис. 4

При этом график функции имеет вид:

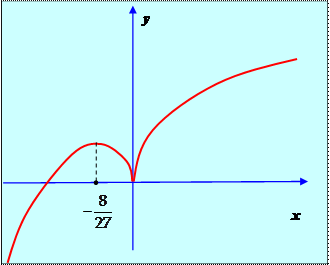
Рис. 5

Ответ: х = 0.

Задача 4.

Найти наименьшее значение функции

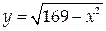
на отрезке [-5,12].

Указание

Функция, непрерывная на отрезке, принимает на нем наименьшее значение либо на границе, либо в критической точке, расположенной внутри отрезка.