Будем называть нормалью прямую, проходящую через данную точку перпендикулярно касательной плоскости, проведенной через эту точку. Тогда канонические уравнения нормали выглядят так:
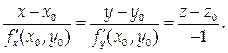
Решение
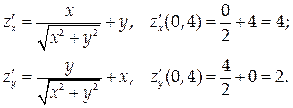
Следовательно, канонические уравнения нормали:
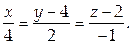
Ответ: 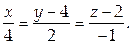
Задача 4.
Найти производную функции
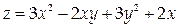
и точке М (2,-4) по направлению вектора MN, если N (-1,-8).
Указание
Производная функции z = f (x, y) в точке (х 0, у 0) по направлению l, заданному вектором а = (ха, уа, za), имеет вид:
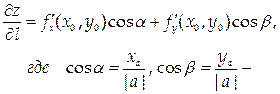
направляющие косинусы направления l.
Решение
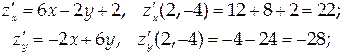
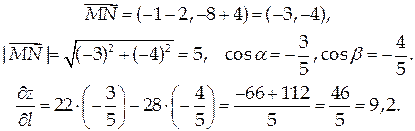
Ответ: 9,2.
Задача 5.
Найти производную функции
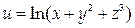
в точке (3,2,1) по направлению, образующему с координатными осями равные тупые углы.
Указание
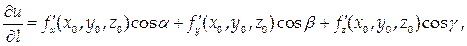
причем
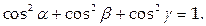
 2015-07-14
2015-07-14 301
301








