Примеры решения задач задания № 14

Решение. По­сколь­ку ка­са­тель­ная па­рал­лель­на пря­мой y = 6 или сов­па­да­ет с ней, их уг­ло­вые ко­эф­фи­ци­ен­ты равны 0. Уг­ло­вой ко­эф­фи­ци­ент ка­са­тель­ной равен зна­че­нию про­из­вод­ной в точке ка­са­ния. Про­из­вод­ная равна нулю в точ­ках экс­тре­му­ма функ­ции. На за­дан­ном ин­тер­ва­ле функ­ция имеет 2 мак­си­му­ма и 2 ми­ни­му­ма, итого 4 экс­тре­му­ма. Таким об­ра­зом, ка­са­тель­ная к гра­фи­ку функ­ции па­рал­лель­на пря­мой y = 6 или сов­па­да­ет с ней в 4-х точ­ках. Ответ: 4.

Задача 14.1 На ри­сун­ке изоб­ра­жен гра­фик функ­ции y = f (x), опре­де­лен­ной на ин­тер­ва­ле (−5; 5). Най­ди­те ко­ли­че­ство точек, в ко­то­рых ка­са­тель­ная к гра­фи­ку функ­ции па­рал­лель­на пря­мой y = 6 или сов­па­да­ет с ней.

Задача 14.2 На ри­сун­ке изоб­ра­жен гра­фик про­из­вод­ной функ­ции 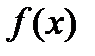, опре­де­лен­ной на ин­тер­ва­ле (−7; 4). В какой точке от­рез­ка [−6; −1] функ­ция 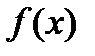при­ни­ма­ет наи­боль­шее зна­че­ние?

Решение. На за­дан­ном от­рез­ке про­из­вод­ная функ­ции по­ло­жи­тель­на, по­это­му функ­ция на этом от­рез­ке воз­рас­та­ет. По­это­му наи­боль­шее зна­че­ние функ­ции до­сти­га­ет­ся на пра­вой гра­ни­це от­рез­ка, т. е. в точке −1. Ответ: −1.

Решение. На за­дан­ном от­рез­ке про­из­вод­ная функ­ции от­ри­ца­тель­на, по­это­му функ­ция на этом от­рез­ке убы­ва­ет. По­это­му наи­мень­шее зна­че­ние функ­ции до­сти­га­ет­ся на пра­вой гра­ни­це от­рез­ка, т. е. в точке 1. Ответ: 1.

Задача 14.3 На ри­сун­ке изоб­ра­жен гра­фик про­из­вод­ной функ­ции f(x), опре­де­лен­ной на ин­тер­ва­ле (−10; 3). В какой точке от­рез­ка [−3; 1] f(x), при­ни­ма­ет наи­мень­шее зна­че­ние?

Задача 14.4 На ри­сун­ке изоб­ра­жен гра­фик про­из­вод­ной функ­ции f(x), опре­де­лен­ной на ин­тер­ва­ле (−7; 10). Най­ди­те ко­ли­че­ство точек ми­ни­му­ма функ­ции f(x) на от­рез­ке [−3; 8].

Решение. Точки ми­ни­му­ма со­от­вет­ству­ют точ­кам смены знака про­из­вод­ной с ми­ну­са на плюс. На от­рез­ке [−3; 8] функ­ция имеет одну точку ми­ни­му­ма x = 4. Ответ: 1.

Задача 14.5 На ри­сун­ке изоб­ра­жен гра­фик про­из­вод­ной функ­ции 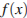, опре­де­лен­ной на ин­тер­ва­ле (−7; 4). Най­ди­те про­ме­жут­ки убы­ва­ния функ­ции .

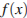В от­ве­те ука­жи­те сумму целых точек, вхо­дя­щих в эти про­ме­жут­ки.

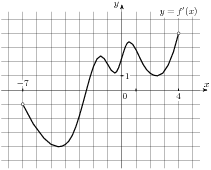
Решение. Про­ме­жут­ки убы­ва­ния функ­ции f (x) со­от­вет­ству­ют про­ме­жут­кам, на ко­то­рых про­из­вод­ная функ­ции от­ри­ца­тель­на, то есть ин­тер­ва­лу (−7; −2,5). Дан­ный ин­тер­вал со­дер­жит сле­ду­ю­щие целые точки: −6, −5, −4, −3, сумма ко­то­рых равна −18. Ответ: −18.