1.1-1.30. Найти производные 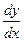 данных функций.
данных функций.
1.1. а) 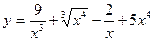 ; б)
; б) 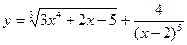 ;
;
в) 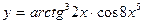 ; г)
; г) 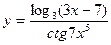 .
.
1.2. а) 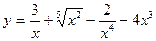 ; б)
; б) 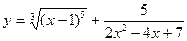 ;
;
в) 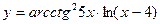 ; г)
; г) 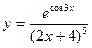 .
.
1.3. а) 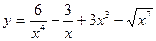 ; б)
; б) 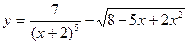 ;
;
в) 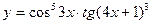 ; г)
; г) 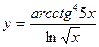 .
.
1.4. а) 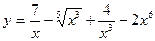 ; б)
; б) 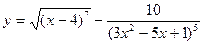 ;
;
в) 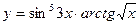 ; г)
; г) 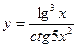 .
.
1.5. а) 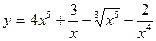 ; б)
; б) 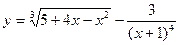 ;
;
в) 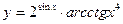 ; г)
; г) 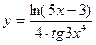 .
.
1.6. а) 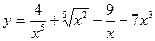 ; б)
; б) 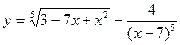 ;
;
в) 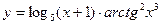 ; г)
; г) 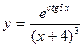 .
.
1.7. а) 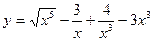 ; б)
; б) 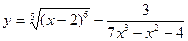 ;
;
в) 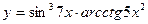 ; г)
; г) 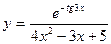 .
.
1.8. а) 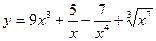 ; б)
; б) 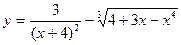 ;
;
в) 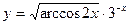 ; г)
; г) 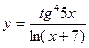 .
.
1.9. а) 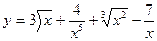 ; б)
; б) 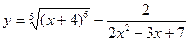 ;
;
в) 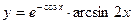 ; г)
; г) 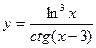 .
.
1.10. а) 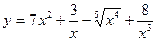 ; б)
; б) 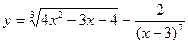 ;
;
в) 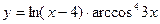 ; г)
; г) 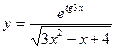 .
.
1.11. а) 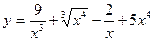 ; б)
; б) 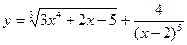 ;
;
в) 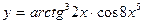 ; г)
; г) 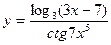 .
.
1.12. а) 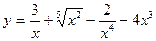 ; б)
; б) 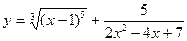 ;
;
в) 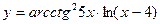 ; г)
; г) 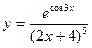 .
.
1.13. а) 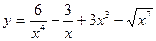 ; б)
; б) 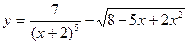 ;
;
в) 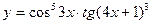 ; г)
; г) 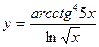 .
.
1.14. а) 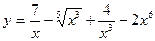 ; б)
; б) 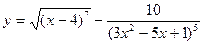 ;
;
в) 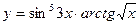 ; г)
; г) 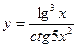 .
.
1.15. а) 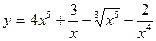 ; б)
; б) 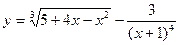 ;
;
в) 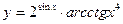 ; г)
; г) 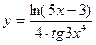 .
.
1.16. а) 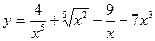 ; б)
; б) 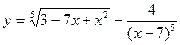 ;
;
в) 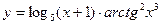 ; г)
; г) 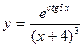 .
.
1.17. а) 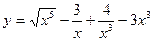 ; б)
; б) 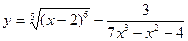 ;
;
в) 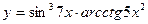 ; г)
; г) 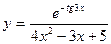 .
.
1.18. а) 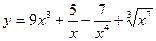 ; б)
; б) 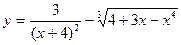 ;
;
в) 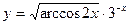 ; г)
; г) 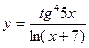 .
.
1.19. а) 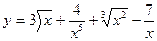 ; б)
; б) 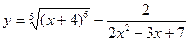 ;
;
в) 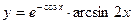 ; г)
; г) 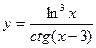 .
.
1.20. а) 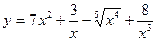 ; б)
; б) 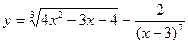 ;
;
в) 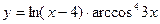 ; г)
; г) 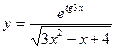 .
.
1.21. а) 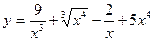 ; б)
; б) 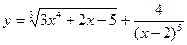 ;
;
в) 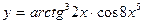 ; г)
; г) 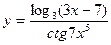 .
.
1.22. а) 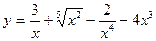 ; б)
; б) 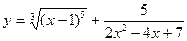 ;
;
в) 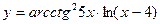 ; г)
; г) 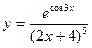 .
.
1.23. а) 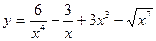 ; б)
; б) 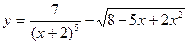 ;
;
в) 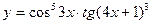 ; г)
; г) 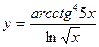 .
.
1.24. а) 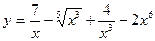 ; б)
; б) 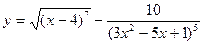 ;
;
в) 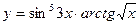 ; г)
; г) 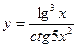 .
.
1.25. а) 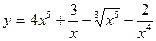 ; б)
; б) 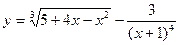 ;
;
в) 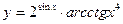 ; г)
; г) 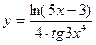 .
.
1.26. а) 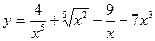 ; б)
; б) 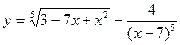 ;
;
в) 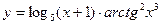 ; г)
; г) 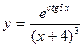 .
.
1.27. а) 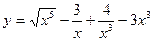 ; б)
; б) 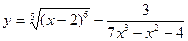 ;
;
в) 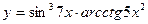 ; г)
; г) 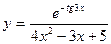 .
.
1.28. а) 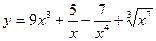 ; б)
; б) 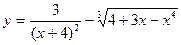 ;
;
в) 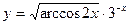 ; г)
; г) 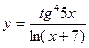 .
.
1.29. а) 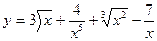 ; б)
; б) 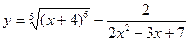 ;
;
в) 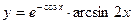 ; г)
; г) 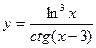 .
.
1.30. а) 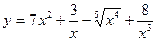 ; б)
; б) 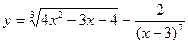 ;
;
в) 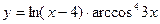 ; г)
; г) 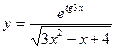 .
.
2.1-2.30. Найти 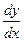 и
и 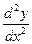 для заданных функций и вычислить их значения в данной точке х0.
для заданных функций и вычислить их значения в данной точке х0.
2.1.  , х0 = 0.
, х0 = 0.
2.2. у = sin2x, x0 = p/2.
2.3. y = ln(2 + x2), x0 = 0.
2.4. y = x4 lnx, x0 = 1.
2.5. y = e xsin2x, x0 = 0.
2.6. y = x sinx, x0 = p/2.
2.7. y = (x+1) ln(x+1), x0 = -1/2.
2.8. y = ln3x, x0 = 1.
2.9. y = e- x cosx, x0 = 0.
2.10. y = x 2 lnx, x0 = 1/3.
2.11.  , х0 = 0.
, х0 = 0.
2.12. у = sin2x, x0 = p/2.
2.13. y = ln(2 + x2), x0 = 0.
2.14. y = x4 lnx, x0 = 1.
2.15. y = e xsin2x, x0 = 0.
2.16. y = x sinx, x0 = p/2.
2.17. y = (x+1) ln(x+1), x0 = -1/2.
2.18. y = ln3x, x0 = 1.
2.19. y = e- x cosx, x0 = 0.
2.20. y = x 2 lnx, x0 = 1/3.
2.21.  , х0 = 0.
, х0 = 0.
2.22. у = sin2x, x0 = p/2.
2.23. y = ln(2 + x2), x0 = 0.
2.24. y = x4 lnx, x0 = 1.
2.25. y = e xsin2x, x0 = 0.
2.26. y = x sinx, x0 = p/2.
2.27. y = (x+1) ln(x+1), x0 = -1/2.
2.28. y = ln3x, x0 = 1.
2.29. y = e- x cosx, x0 = 0.
2.30. y = x 2 lnx, x0 = 1/3.
3.1-3.30. Найти дифференциалы первого и второго порядка для заданных функций и вычислить их значения в заданной точке х0.
3.1.  , х0 = 0.
, х0 = 0.
3.2. 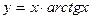 , х0 =1.
, х0 =1.
3.3. 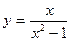 , х0 = 0.
, х0 = 0.
3.4. 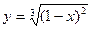 , х0 = 2.
, х0 = 2.
3.5. 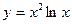 , х0 =1.
, х0 =1.
3.6. 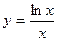 , х0 = 1.
, х0 = 1.
3.7. 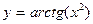 , х0 = -1.
, х0 = -1.
3.8. 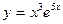 , х0 = 0.
, х0 = 0.
3.9. 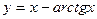 , х0 = -1.
, х0 = -1.
3.10. 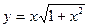 , х0 = 0.
, х0 = 0.
3.11.  , х0 = 0.
, х0 = 0.
3.12. 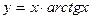 , х0 =1.
, х0 =1.
3.13. 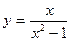 , х0 = 0.
, х0 = 0.
3.14. 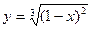 , х0 = 2.
, х0 = 2.
3.15. 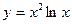 , х0 =1.
, х0 =1.
3.16. 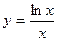 , х0 = 1.
, х0 = 1.
3.17. 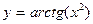 , х0 = -1.
, х0 = -1.
3.18. 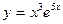 , х0 = 0.
, х0 = 0.
3.19. 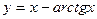 , х0 = -1.
, х0 = -1.
3.20. 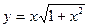 , х0 = 0.
, х0 = 0.
3.21.  , х0 = 0.
, х0 = 0.
3.22. 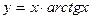 , х0 =1.
, х0 =1.
3.23. 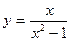 , х0 = 0.
, х0 = 0.
3.24. 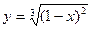 , х0 = 2.
, х0 = 2.
3.25. 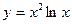 , х0 =1.
, х0 =1.
3.26. 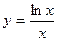 , х0 = 1.
, х0 = 1.
3.27. 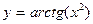 , х0 = -1.
, х0 = -1.
3.28. 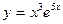 , х0 = 0.
, х0 = 0.
3.29. 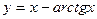 , х0 = -1.
, х0 = -1.
3.30. 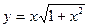 , х0 = 0.
, х0 = 0.
4.1. Проверитьсправедливость теоремы Ролля для функции y = 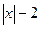 на данном отрезке [–2;2]. Найти соответствующее значение с (если оно существует).
на данном отрезке [–2;2]. Найти соответствующее значение с (если оно существует).
4.2. Найти точку, в которой касательная к кривой y = x2 – 4x параллельно хорде, соединяющей точки А (1, –3) и В (5,5). Сделать поясняющий рисунок.
4.3. Проверить справедливость теоремы Лагранжа для функции y=еx на данном отрезке [0,1]. Найти соответствующее значение с (если оно существует).
4.4. Дана функция y = 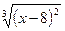 . Пусть а = 0, b = 16. Тогда y(0) = y (16) = 4. Однако производная этой функции не обращается в нуль ни в одной точке интервала (0,16). Противоречит ли это теореме Ролля?
. Пусть а = 0, b = 16. Тогда y(0) = y (16) = 4. Однако производная этой функции не обращается в нуль ни в одной точке интервала (0,16). Противоречит ли это теореме Ролля?
4.5. Проверитьсправедливость теоремы Ролля для функции y = –x2 + 4x –3 на данном отрезке [0,4]. Найти соответствующее значение с (если оно существует).
4.6. Найти точку, в которой касательная к кривой y = ln x параллельно хорде, соединяющей точки А (1, 0) и В (е,1). Сделать поясняющий рисунок.
4.7. Проверить справедливость теоремы Лагранжа для функции y = 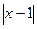 на данном отрезке [0,3]. Найти соответствующее значение с (если оно существует).
на данном отрезке [0,3]. Найти соответствующее значение с (если оно существует).
4.8. Проверитьсправедливость теоремы Ролля для функции y = 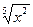 на данном отрезке [1,1]. Найти соответствующее значение с (если оно существует).
на данном отрезке [1,1]. Найти соответствующее значение с (если оно существует).
4.9. Проверить справедливость теоремы Лагранжа для функции y= 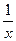 на данном отрезке [
на данном отрезке [ 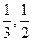 ]. Найти соответствующее значение с (если оно существует).
]. Найти соответствующее значение с (если оно существует).
4.10. Проверитьсправедливость теоремы Ролля для функции y = cos x на данном отрезке [ 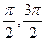 ]. Найти соответствующее значение с (если оно существует).
]. Найти соответствующее значение с (если оно существует).
4.11. Проверитьсправедливость теоремы Ролля для функции y = 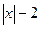 на данном отрезке [–2;2]. Найти соответствующее значение с (если оно существует).
на данном отрезке [–2;2]. Найти соответствующее значение с (если оно существует).
4.12. Найти точку, в которой касательная к кривой y = x2 – 4x параллельно хорде, соединяющей точки А (1, –3) и В (5,5). Сделать поясняющий рисунок.
4.13. Проверить справедливость теоремы Лагранжа для функции y=еx на данном отрезке [0,1]. Найти соответствующее значение с (если оно существует).
4.14. Дана функция y = 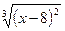 . Пусть а = 0, b = 16. Тогда y(0) = y (16) = 4. Однако производная этой функции не обращается в нуль ни в одной точке интервала (0,16). Противоречит ли это теореме Ролля?
. Пусть а = 0, b = 16. Тогда y(0) = y (16) = 4. Однако производная этой функции не обращается в нуль ни в одной точке интервала (0,16). Противоречит ли это теореме Ролля?
4.15. Проверитьсправедливость теоремы Ролля для функции y = –x2 + 4x –3 на данном отрезке [0,4]. Найти соответствующее значение с (если оно существует).
4.16. Найти точку, в которой касательная к кривой y = ln x параллельно хорде, соединяющей точки А (1, 0) и В (е,1). Сделать поясняющий рисунок.
4.17. Проверить справедливость теоремы Лагранжа для функции y = 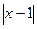 на данном отрезке [0,3]. Найти соответствующее значение с (если оно существует).
на данном отрезке [0,3]. Найти соответствующее значение с (если оно существует).
4.18. Проверитьсправедливость теоремы Ролля для функции y = 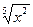 на данном отрезке [1,1]. Найти соответствующее значение с (если оно существует).
на данном отрезке [1,1]. Найти соответствующее значение с (если оно существует).
4.19. Проверить справедливость теоремы Лагранжа для функции y= 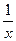 на данном отрезке [
на данном отрезке [ 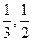 ]. Найти соответствующее значение с (если оно существует).
]. Найти соответствующее значение с (если оно существует).
4.20. Проверитьсправедливость теоремы Ролля для функции y = cos x на данном отрезке [ 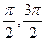 ]. Найти соответствующее значение с (если оно существует).
]. Найти соответствующее значение с (если оно существует).
4.21. Проверитьсправедливость теоремы Ролля для функции y = 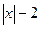 на данном отрезке [–2;2]. Найти соответствующее значение с (если оно существует).
на данном отрезке [–2;2]. Найти соответствующее значение с (если оно существует).
4.22. Найти точку, в которой касательная к кривой y = x2 – 4x параллельно хорде, соединяющей точки А (1, –3) и В (5,5). Сделать поясняющий рисунок.
4.23. Проверить справедливость теоремы Лагранжа для функции y=еx на данном отрезке [0,1]. Найти соответствующее значение с (если оно существует).
4.24. Дана функция y = 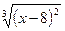 . Пусть а = 0, b = 16. Тогда y(0) = y (16) = 4. Однако производная этой функции не обращается в нуль ни в одной точке интервала (0,16). Противоречит ли это теореме Ролля?
. Пусть а = 0, b = 16. Тогда y(0) = y (16) = 4. Однако производная этой функции не обращается в нуль ни в одной точке интервала (0,16). Противоречит ли это теореме Ролля?
4.25. Проверитьсправедливость теоремы Ролля для функции y = –x2 + 4x –3 на данном отрезке [0,4]. Найти соответствующее значение с (если оно существует).
4.26. Найти точку, в которой касательная к кривой y = ln x параллельно хорде, соединяющей точки А (1, 0) и В (е,1). Сделать поясняющий рисунок.
4.27. Проверить справедливость теоремы Лагранжа для функции y = 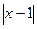 на данном отрезке [0,3]. Найти соответствующее значение с (если оно существует).
на данном отрезке [0,3]. Найти соответствующее значение с (если оно существует).
4.28. Проверитьсправедливость теоремы Ролля для функции y = 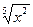 на данном отрезке [1,1]. Найти соответствующее значение с (если оно существует).
на данном отрезке [1,1]. Найти соответствующее значение с (если оно существует).
4.29. Проверить справедливость теоремы Лагранжа для функции y= 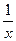 на данном отрезке [
на данном отрезке [ 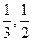 ]. Найти соответствующее значение с (если оно существует).
]. Найти соответствующее значение с (если оно существует).
4.30. Проверитьсправедливость теоремы Ролля для функции y = cos x на данном отрезке [ 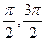 ]. Найти соответствующее значение с (если оно существует).
]. Найти соответствующее значение с (если оно существует).
5.1-5.30. Найти пределы, используя правило Лопиталя.
5.1. 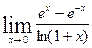 . 5.16.
. 5.16. 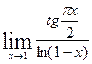 .
.
5.2. 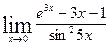 . 5.17.
. 5.17. 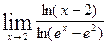 .
.
5.3. 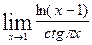 . 5.18.
. 5.18. 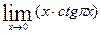 .
.
5.4. 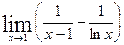 . 5.19.
. 5.19. 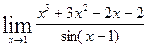 .
.
5.5. 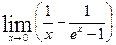 . 5.20.
. 5.20. 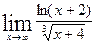 .
.
5.6. 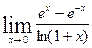 . 5.21.
. 5.21. 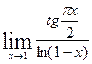 .
.
5.7. 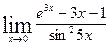 . 127.
. 127. 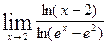 .
.
5.8. 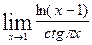 . 128.
. 128. 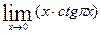 .
.
5.9. 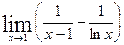 . 129.
. 129. 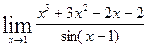 .
.
5.10. 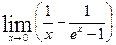 . 130.
. 130. 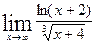 .
.
5.11. 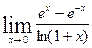 . 126.
. 126. 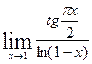 .
.
5.12. 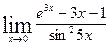 . 127.
. 127. 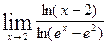 .
.
5.13. 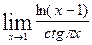 . 128.
. 128. 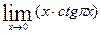 .
.
5.14. 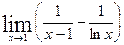 . 129.
. 129. 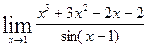 .
.
5.15. 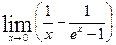 . 130.
. 130. 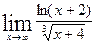 .
.
6.1.-6.30. Исследовать методами дифференциального исчисления функцию 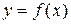 и, используя результаты исследования, построить их графики.
и, используя результаты исследования, построить их графики.
6.1. а) 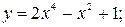 б)
б) 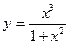
6.2. а) 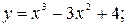 б)
б) 
6.3. а) 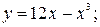 б)
б) 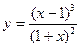
6.4. а) 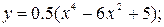 б)
б) 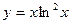
6.5. а) 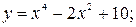 б)
б) 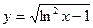
6.6. а) 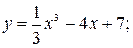 б)
б) 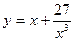
6.7. а) 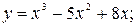 б)
б) 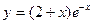
6.8. а) 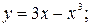 б)
б) 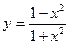
6.9. а) 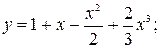 б)
б) 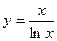
6.10. а) 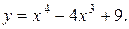 б)
б) 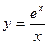
6.11. а) 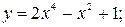 б)
б) 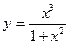
6.12. а) 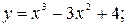 б)
б) 
6.13. а) 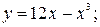 б)
б) 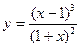
6.14. а) 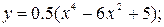 б)
б) 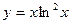
6.15. а) 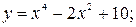 б)
б) 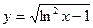
6.16. а) 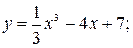 б)
б) 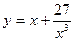
6.17. а) 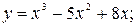 б)
б) 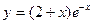
6.18. а) 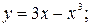 б)
б) 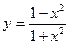
6.19. а) 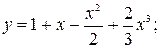 б)
б) 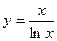
6.20. а) 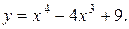 б)
б) 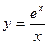
6.21. а) 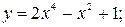 б)
б) 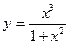
6.22. а) 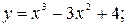 б)
б) 
6.23. а) 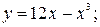 б)
б) 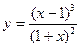
6.24. а) 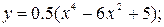 б)
б) 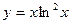
6.25. а) 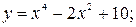 б)
б) 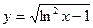
6.26. а) 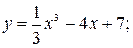 б)
б) 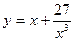
6.27. а) 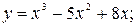 б)
б) 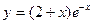
6.28. а) 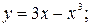 б)
б) 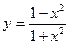
6.29. а) 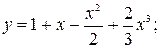 б)
б) 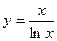
6.30. а) 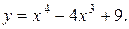 б)
б) 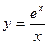
 2015-07-14
2015-07-14 524
524







