Для нахождения производной показательной функции воспользуемся правилом дифференцирования обратной функции.
Если 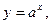 то
то 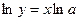 и
и 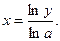
Отсюда 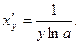
Следовательно, 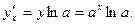
Таким образом, 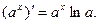
В частности, если 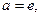 то
то 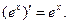
Примеры.
1. 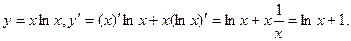
2. 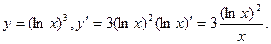
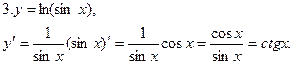
4. 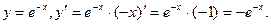
Таблица основных формул дифференцирования.
На этом этапе темы «Производная» целесообразно составить следующую таблицу производных 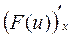 , где F – одна из основных элементарных функций. Напомним, что основными элементарными функциями принято называть следующие: степенную функцию
, где F – одна из основных элементарных функций. Напомним, что основными элементарными функциями принято называть следующие: степенную функцию 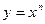 , показательную функцию
, показательную функцию  , логарифмическую функцию
, логарифмическую функцию 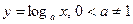 , четыре
, четыре
тригонометрические функции 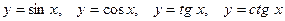 и четыре обратные тригонометрические функции
и четыре обратные тригонометрические функции 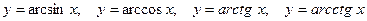 .
.
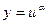
| 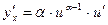
| |
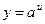
| 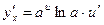
| |
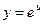
| 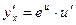
| |
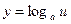
| 
| |
| 
| |
| 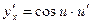
| |
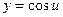
| 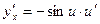
| |
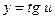
| 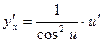
| |
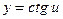
| 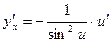
| |
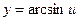
| 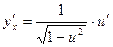
| |
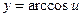
| 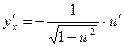
| |
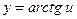
| 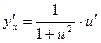
| |
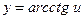
| 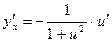
|
 2015-07-14
2015-07-14 311
311








