Если 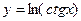 ,то
,то
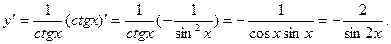
Производные обратных тригонометрических функций.
Пусть y=arcsinx, где -1≤x≤1 и 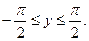
Обратная функция имеет вид x=siny, причем 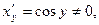 если
если 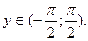
Используя правило дифференцирования обратной
функции, получим
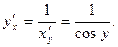
Так как 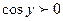 при
при 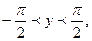 то, получаем
то, получаем 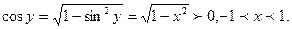
Следовательно, имеем 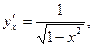 т.е. (
т.е. (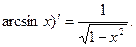
2. Пусть y=arccosx, тогда x=cosy, причем -1≤x≤1 и 0≤y≤π.
На основании правила дифференцирования обратной функции имеем
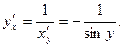
Так как siny>0 при 0<y<π, то 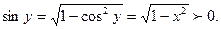
Поэтому 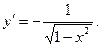
Таким образом, 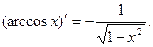
3.Пусть y=arctgx 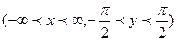 и, следовательно, x=tgy.
и, следовательно, x=tgy.
Имеем 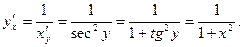
Таким образом, 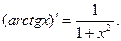
4.Пусть y=arcctgx 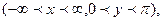
тогда x=ctgy.
Имеем 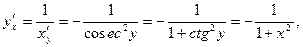
т.е. 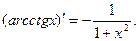
Пример.
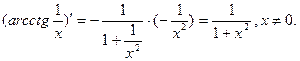
 2015-07-14
2015-07-14 326
326








