Пусть функция f(x, y) дифференцируема в точке (х, у). Найдем полное приращение этой функции:
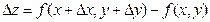
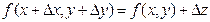
Если подставить в эту формулу выражение
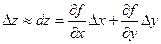
то получим приближенную формулу:
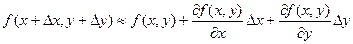
Пример. Вычислить приближенно значение 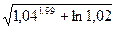 , исходя из значения функции
, исходя из значения функции 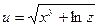 при x = 1, y = 2, z = 1.
при x = 1, y = 2, z = 1.
Из заданного выражения определим Dx = 1,04 – 1 = 0,04, Dy = 1,99 – 2 = -0,01,
Dz = 1,02 – 1 = 0,02.
Найдем значение функции u(x, y, z) = 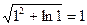
Находим частные производные:
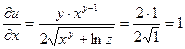
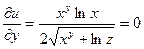
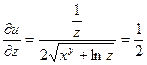
Полный дифференциал функции u равен:
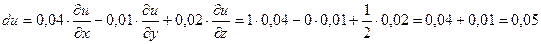
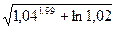
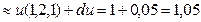
Точное значение этого выражения: 1,049275225687319176.
Вычислить приближенно с помощью дифференциала 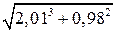 .
.
Решение. Введем функцию двух переменных 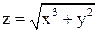 . Так как 2,01=2+0,01,
. Так как 2,01=2+0,01, 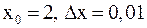 . Аналогично
. Аналогично 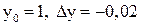 , т. к.
, т. к. 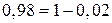 . Воспользуемся тем, что
. Воспользуемся тем, что 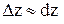 при малых
при малых 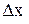 и
и 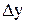 .
.
Так как 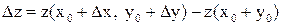 ,
,
отсюда следует, что 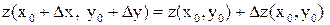 .
.
Заменим приращение функции 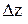 ее дифференциалом
ее дифференциалом 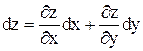 ,
,
где 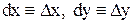 .
.
Тогда 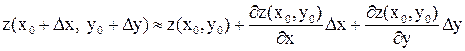 ,
,
т. е. в данном случае 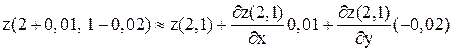 .
.
Вычислим 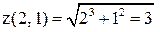 . Найдем
. Найдем 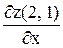 . Для этого сначала найдем частную производную
. Для этого сначала найдем частную производную 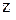 по
по 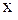 в произвольной точке.
в произвольной точке.
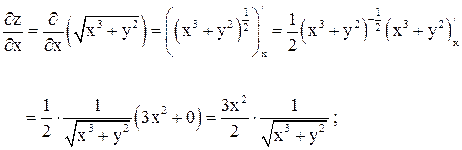
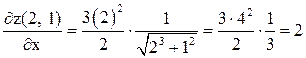 .
.
Теперь найдем
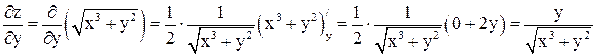 ;
;
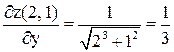 .
.
Находим искомое значение корня
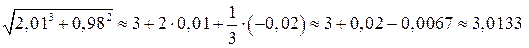 .
.
Если найти 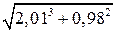 на калькуляторе, то получим
на калькуляторе, то получим 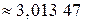 . Различие только в четвертом знаке после запятой.
. Различие только в четвертом знаке после запятой.
Ответ: 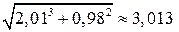 .
.
 2015-07-14
2015-07-14 2326
2326






