 Рассмотрим поле, создаваемое сферической поверхностью радиуса R, заряженной с постоянной поверхностной плотностью
Рассмотрим поле, создаваемое сферической поверхностью радиуса R, заряженной с постоянной поверхностной плотностью 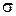 . Это поле обладает центральной симметрией. Это означает, что направление вектора
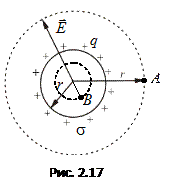
. Это поле обладает центральной симметрией. Это означает, что направление вектора 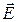 в любой точке проходит через центр сферы, а значение напряженности является функцией расстояния r от центра сферы (рис. 2.17). Найдем напряженность поля, созданную заряженной сферой в точках А и В. Через точки А и В проведем сферические поверхности и найдем поток вектора напряженности через эти поверхности.
в любой точке проходит через центр сферы, а значение напряженности является функцией расстояния r от центра сферы (рис. 2.17). Найдем напряженность поля, созданную заряженной сферой в точках А и В. Через точки А и В проведем сферические поверхности и найдем поток вектора напряженности через эти поверхности.
Точка В находится внутри заряженной сферической поверхности, на расстоянии r от центра (r<R). Сферическая поверхность, проведенная через эту точку, не будет содержать внутри заряда. Следовательно, по теореме Гаусса 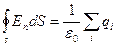 , напряженность в точке В будет равна нулю. Е =0 (r<R) (рис. 2.17).Найдем напряженность поля, созданного заряженной сферической поверхностью в точке А, находящейся на расстоянии r от центра сферы. Окружим заряженное тело замкнутой сферической поверхностью, радиуса r, проходящей через точку А (рис. 2.17).
, напряженность в точке В будет равна нулю. Е =0 (r<R) (рис. 2.17).Найдем напряженность поля, созданного заряженной сферической поверхностью в точке А, находящейся на расстоянии r от центра сферы. Окружим заряженное тело замкнутой сферической поверхностью, радиуса r, проходящей через точку А (рис. 2.17).
Для всех точек этой поверхности 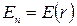 . Внутрь поверхности попадает весь заряд q, создающий рассматриваемое поле. Следовательно,
. Внутрь поверхности попадает весь заряд q, создающий рассматриваемое поле. Следовательно, 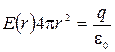 (так как
(так как 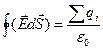 ).
).
Таким образом, напряженность поля в точках, расположенных на расстоянии r>R, равна
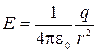 Поле вне заряженной сферической поверхности имеет такой же вид, как поле точечного заряда q, находящегося на расстоянии r от точки А. Если известна поверхностная плотность заряда σ, то
Поле вне заряженной сферической поверхности имеет такой же вид, как поле точечного заряда q, находящегося на расстоянии r от точки А. Если известна поверхностная плотность заряда σ, то 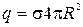 , подставив в (8), получим
, подставив в (8), получим
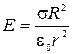 .
.
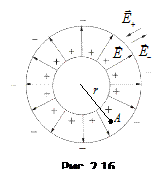
Рассчитаем напряженность поля, создаваемого бесконечно длинным цилиндром радиуса R, заряженным с поверхностной плотностью 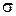 в точке А, отстоящей на расстояния r от оси цилиндра. Из соображений симметрии следует, что напряженность в любой точке направлена вдоль радиальной прямой, перпендикулярной к оси цилиндра, а значение напряженности зависит лишь от расстояния r от цилиндра. Вырежем из бесконечно длинного цилиндра элемент длиной h. Окружим этот элемент цилиндрической поверхностью (коаксиальной с заряженной) радиуса r, так, чтобы эта поверхность проходила через точку А (рис. 2.15). Для оснований внешнего цилиндра
в точке А, отстоящей на расстояния r от оси цилиндра. Из соображений симметрии следует, что напряженность в любой точке направлена вдоль радиальной прямой, перпендикулярной к оси цилиндра, а значение напряженности зависит лишь от расстояния r от цилиндра. Вырежем из бесконечно длинного цилиндра элемент длиной h. Окружим этот элемент цилиндрической поверхностью (коаксиальной с заряженной) радиуса r, так, чтобы эта поверхность проходила через точку А (рис. 2.15). Для оснований внешнего цилиндра 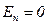 , для боковой поверхности (заряд считаем положительным)
, для боковой поверхности (заряд считаем положительным) 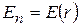 . Силовые линии поля пересекают только боковую поверхность цилиндра радиуса r. Следовательно, поток вектора
. Силовые линии поля пересекают только боковую поверхность цилиндра радиуса r. Следовательно, поток вектора 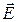 через эту замкнутую поверхность будет равен
через эту замкнутую поверхность будет равен 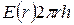 . Если
. Если 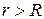 внутрь поверхности попадает заряд
внутрь поверхности попадает заряд 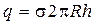 , где
, где 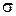 –поверхностная плотность заряда. Применяя теорему Гаусса, получаем:
–поверхностная плотность заряда. Применяя теорему Гаусса, получаем:
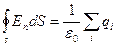 ,
, 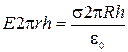 , откуда
, откуда 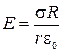 . (5)
. (5)
Если 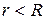 , рассматриваемая замкнутая поверхность не содержит внутри зарядов, вследствие чего
, рассматриваемая замкнутая поверхность не содержит внутри зарядов, вследствие чего 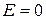 . Таким образом, внутри заряженной цилиндрической поверхности поле отсутствует.
. Таким образом, внутри заряженной цилиндрической поверхности поле отсутствует.
Если радиус цилиндра 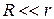 , а заряд распределяется по длине цилиндра с линейной плотностью τ. Тогда можно формулу (17) преобразовать:
, а заряд распределяется по длине цилиндра с линейной плотностью τ. Тогда можно формулу (17) преобразовать:
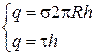
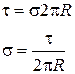 Тогда
Тогда 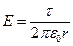
 2015-07-14
2015-07-14 8211
8211
