Энергия заряженного конденсатора. Применение конденсаторов

Как и любая система заряжен­ных тел, конденсатор обладает энер­гией. Вычислить энергию заряжен­ного плоского конденсатора с одно­родным полем внутри него не­сложно.

Энергия заряженного конденса­тора.

Для того чтобы зарядить конденсатор, нужно совершить рабо­ту по разделению положительных и отрицательных зарядов. Согласно закону сохранения энергии эта ра­бота равна энергии конденсатора. В том, что заряженный конденсатор обладает энергией, можно убедиться, если разрядить его через цепь, со­держащую лампу накаливания, рас­считанную на напряжение в не­сколько вольт (рис. 4). При раз­рядке конденсатора лампа вспыхи­вает. Энергия конденсатора пре­вращается в другие формы: тепло­вую, световую.

Выведем формулу для энергии плоского конденсатора.

Напряженность поля, созданного зарядом одной из пластин, равна Е/2, где Е — напряженность поля в конденсаторе. В однородном поле одной пластины находится заряд q, распределенный по поверхности дру­гой пластины (рис. 5). Согласно формуле W_p = qEd. для потенциальной энергии заряда в однородном поле энергия конденсатора равна:

 

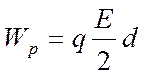(1)

где q — заряд конденсатора, a d — расстояние между пластинами.

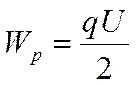
Так как Ed = U, где U — разность потенциалов между обкладка­ми конденсатора, то его энергия равна:

(2)

Эта энергия равна работе, ко­торую совершит электрическое поле при сближении пластин вплот­ную.

Заменив в формуле (2) раз­ность потенциалов или заряд с по­мощью выражения для элек­троемкости конденсатора, получим

 

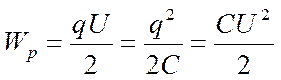(3)

Можно доказать, что эти форму­лы справедливы для энергии любого конденсатора, а не только для плос­кого.

Энергия электрического поля.

Согласно теории близкодействия вся энергия взаимодействия заряженных тел сконцентрирована в электриче­ском поле этих тел. Значит, энергия может быть выражена через основную характеристику поля — напря­женность.

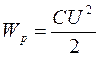
Так как напряженность электри­ческого поля прямо пропорциональ­на разности потенциалов

(U = Ed), то согласно формуле

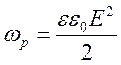
энергия конденсатора прямо пропор­циональна напряженности электри­ческого поля внутри него: W_p ~ E². Детальный расчет дает следующее значение для энергии поля, приходя­щейся на единицу объема, т.е. для плотности энергии:

(4)

где ε₀ — электрическая постоянная

Применение конденсаторов.

Энер­гия конденсатора обычно не очень велика — не более сотен джоулей. К тому же она не сохраняется долго из-за неизбежной утечки заряда. Поэтому заряженные конденсаторы не могут заменить, например, акку­муляторы в качестве источников электрической энергии.

Но это совсем не означает, что конденсаторы как накопители энергии не получили практического при­менения. Они имеют одно важное свойство: конденсаторы могут на­капливать энергию более или менее длительное время, а при разрядке через цепь малого сопротивления они отдают энергию почти мгновенно. Именно это свойство используют широко на практике.

Лампа-вспышка, применяемая в фотографии, питается электрическим током разряда конденсатора, заря­жаемого предварительно специаль­ной батареей. Возбуждение кванто­вых источников света — лазеров осу­ществляется с помощью газораз­рядной трубки, вспышка которой происходит при разрядке батареи конденсаторов большой электроем­кости.

Однако основное применение кон­денсаторы находят в радиотехнике. С этим вы познакомитесь в XI классе.

Энергия конденсатора пропор­циональна его электроемкости и квадрату напряжения между плас­тинами. Вся эта энергия сосредото­чена в электрическом поле. Плот­ность энергии поля пропорциональна квадрату напряженности поля.

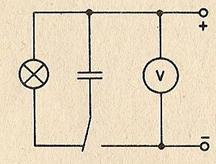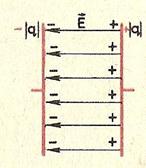Рис. 1 Рис. 2

ЗАКОНЫ ПОСТОЯННОГО ТОКА.

Неподвижные электрические заряды редко используются на практике. Для того чтобы заставить электрические заряды слу­жить нам, их нужно привести в движение — создать электрический ток. Электрический ток освещает квартиры, приводит в дви­жение станки, создает радиоволны, циркулирует во всех электрон­но-вычислительных машинах.

Мы начнем с наиболее простого случая движения заряжен­ных частиц — рассмотрим постоянный электрический ток.

ЭЛЕКТРИЧЕСКИЙ ТОК. СИЛА ТОКА

Дадим строгое определение тому, что называют электрическим током.

Напомним, какой величиной ха­рактеризуется ток количественно.

Найдем, как быстро движутся электроны по проводам в вашей квартире.

При движении заряженных час­тиц в проводнике происходит перенос электрического заряда с одного места в другое. Однако если заряженные частицы совершают беспорядочное тепловое движение, как, например, свободные электроны в металле, то переноса заряда не про­исходит (рис.1). Электриче­ский заряд перемещается через по­перечное сечение проводника лишь в том случае, если наряду с беспорядочным движением электроны участвуют в упорядоченном движении (рис. 2 ). В этом случае говорят, что в проводнике устанавливается электрический ток.

Из курса физики VIII класса вы знаете, что электрическим током называют упорядоченное (направ­ленное) движение заряженных частиц.

Электрический ток возникает при упорядоченном перемещении свобод­ных электронов или ионов.

Если перемещать нейтральное в целом тело, то, несмотря на упо­рядоченное движение огромного чис­ла электронов, и атомных ядер, электрический ток не возникает. Полный заряд, переносимый через любое сечение проводника, будет при этом равным нулю, так как заряды разных знаков с одинаковой средней скоростью.

Электрический ток имеет определенное направление. За направление тока принимают направление движения положительно заряженных частиц. Если ток образован движением отрицательно заряженных частиц, то направление тока считают противоположным направлению дви­жения частиц.

Действия тока. Движение частиц в проводнике мы непосредственно не видим. О наличии электрического тока приходится судить по тем дей­ствиям или явлениям, которые его сопровождают.

Во-первых, проводник, по которо­му течет ток, нагревается.

Во-вторых, электрический ток мо­жет изменять химический состав проводника, например, выделять его химические составные части (медь из раствора медного купороса и т.д.).

В-третьих, ток оказывает силовое воздействие на соседние токи и на­магниченные тела. Это действие то­ка называется магнитным. Так, маг­нитная стрелка вблизи проводника с током поворачивается. Магнитное действие тока в отличие от химиче­ского и теплового является основ­ным, так как проявляется у всех без исключения проводников. Хими­ческое действие тока наблюдается лишь у растворов и расплавов электролитов, а нагревание отсут­ствует у сверхпроводников.

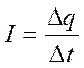
Сила тока.

Если в цепи уста­навливается электрический ток, то это означает, что через поперечное сечение проводника все время пере­носится электрический заряд. Заряд, перенесенный в единицу времени, служит основной количественной ха­рактеристикой тока, называемой си­лой тока.

Таким образом, сила тока равна отношению заряда q, переносимого через поперечное сечение провод­ника за интервал времени t, к этому интервалу времени. Если сила тока со временем не меняется, то ток на­зывают постоянным.

Сила тока, подобно заряду, — ве­личина скалярная. Она может быть как положительной, так и отрица­тельной. Знак силы тока зависит от того, какое из направлений вдоль проводника принять за положитель­ное. Сила тока / > 0, если направ­ление тока совпадает с условно вы­бранным положительным направле­нием вдоль проводника. В против­ном случае / < 0.

Сила тока зависит от заряда, переносимого каждой частицей, кон­центрации частиц, скорости их направленного движения и площади поперечного сечения проводника. По­кажем это.

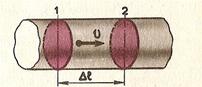
Пусть проводник (рис. 3) имеет поперечное сечение площадью S. За положительное направление в проводнике примем направление сле­ва направо. Заряд каждой частицы равен q₀. В объеме проводника, ограниченном поперечными сечениям­и 1 и 2, содержится nSl частиц, где п — концентрация частиц. Их общий заряд q = q_QnSl. Если частицы движутся слева направо со средней скоростью υ, то за время

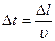все частицы, заключенные в рассматриваемом объеме, пройдут через поперечное сечение 2. Поэтому сила тока равна:

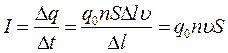В Международной системе еди­ниц силу тока выражают в ампеpax (А). Эту единицу устанавливают наоснове магнитного взаимодей­ствия токов. Измеряют силу тока амперметрами. С принципом устрой­ства этих приборов, основанным на магнитном действии тока, мы позна­комимся позднее.

Скорость упорядоченного движе­ния электронов в проводнике.

Най­дем скорость упорядоченного пере­мещения электронов в металличе­ском проводнике. Согласно

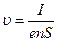формуле (2) где е — модуль заряда электрона.

Пусть, например, сила тока I = 1 А, а площадь по­перечного сечения проводника S = 10 ^-6 м². Модуль заряда электрона е = 1,6 - 10 ^-19 Кл. Число электронов в 1 м³ меди равно числу атомов в этом объеме, так как один из ва­лентных электронов каждого атома меди коллективизирован и является свободным. Это число есть п = 8,5 · 10²⁸ м ^-3 Следовательно,

 

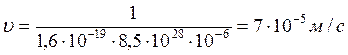Как видите, скорость упорядочен­ного перемещения электронов очень мала.

Основная количественная харак­теристика электрического тока - сила тока. Она определяется электри­ческим зарядом, переносимым через поперечное сечение проводника за единицу времени. Скорость заряжен­ных частиц (электронов) в провод­нике очень мала - около 0,1 мм/с.

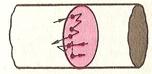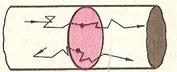Рис №1. Рис №2 Рис №3

УСЛОВИЯ, НЕОБХОДИМЫЕ ДЛЯ СУЩЕСТВОВАНИЯ ЭЛЕКТРИЧЕСКОГО ТОКА

Что необходимо для создания электрического тока? Подумайте над этим сами и только потом прочтите этот параграф.

Для возникновения и существо­вания постоянного электрического тока в веществе необходимо, во-первых, наличие свободных заряжен­ных частиц. Если положительные и отрицательные заряды связаны друг с другом в атомах или молекулах, то их перемещение не приведет к по­явлению электрического тока.

Наличия свободных зарядов еще недостаточно для возникновения то­ка. Для создания и поддержания упорядоченного движения, заряжен­ных частиц необходима, во-вторых, сила, действующая на них в опре­деленном направлении. Если эта сила перестанет действовать, то упорядоченное движение заряженных частиц прекратится из-за сопротив­ления, оказываемого их движению ионами кристаллической решетки металлов или нейтральными молеку­лами электролитов.

На заряженные частицы, как мы знаем, действует электрическое поле с силой 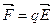. Обычно именно электрическое поле внутри провод­ника служит причиной, вызываю­щей и поддерживающей упорядочен­ное движение заряженных частиц. Только в статическом случае, когда заряды покоятся, электрическое поле внутри проводника равно нулю.

Если внутри проводника имеется электрическое поле, то между конца­ми проводника в соответствии с фор­мулой существует разность потенциалов. Когда разность потен­циалов не меняется во времени, то в проводнике устанавливается по­стоянный электрический ток. Вдоль проводника потенциал уменьшается от максимального значения на одном конце проводника до минималь­ного — на другом. Это уменьшение потенциала можно обнаружить на простом опыте.

Возьмем в качестве проводника не очень сухую деревянную палку и подвесим ее горизонтально. (Такая палка хотя и плохо, но все же про­водит ток.) Источником напряжения пусть будет электростатическая ма­шина, Для регистрации потенциала различных участков проводника от­носительно земли можно использо­вать листочки металлической фоль­ги, прикрепленные к палке. Один полюс машины соединим с землей, а второй — с одним концом проводни­ка (палки). Цепь окажется незамк­нутой. При вращении рукоятки ма­шины мы обнаружим, что все лис­точки отклоняются на один и тот же угол (рис. 1 ).

Значит, потен­циал всех точек проводника отно­сительно земли одинаков. Так и должно быть при равновесии заря­дов на проводнике. Если теперь дру­гой конец палки заземлить, то при вращении рукоятки машины карти­на изменится. (Так как земля — проводник, то заземление провод­ника делает цепь замкнутой.) У за­земленного конца листочки вообще не разойдутся: потенциал этого кон­ца проводника практически равен потенциалу земли (падение потен­циала в металлической проволоке мало). Максимальный угол расхож­дения листочков будет у конца про­водника, присоединенного к машине (рис. 2). Уменьшение угла рас­хождения листочков по мере удале­ния от машины свидетельствует о падении потенциала вдоль провод­ника.

Электрический ток может быть получен только в веществе, в котором имеются свободные заряженные частицы. Чтобы они пришли в движение, нужно создать в проводнике электрическое поле.

Рис №1 Рис №2

ЗАКОН ОМА ДЛЯ УЧАСТКА ЦЕПИ. СОПРОТИВЛЕНИЕ

В VIII классе изучался закон Ома. Этот закон прост, однако столь важен, что его необходимо повторить.

Вольт - амперная характеристика.

В предыдущем параграфе было уста­новлено, что для существования то­ка в проводнике необходимо создать разность потенциалов на его концах. Сила тока в проводнике определяет­ся этой разностью потенциалов. Чем больше разность потенциалов, тем больше напряженность электриче­ского поля в проводнике и, следо­вательно, тем большую скорость на­правленного движения приобретают заряженные частицы. Согласно фор­муле, это означает увеличение силы тока.

Для каждого проводника — твер­дого, жидкого и газообразного — существует определенная зависи­мость силы тока от приложенной разности потенциалов на концах про­водника. Эту зависимость выражает так называемая вольт - амперная ха­рактеристика проводника. Ее нахо­дят, измеряя силу тока в проводнике при различных значениях напряже­ния. Знание вольт - амперной характе­ристики играет большую роль при изучении электрического тока.

Закон Ома.

Наиболее простой вид имеет вольт - амперная характеристи­ка металлических проводников и растворов электролитов. Впервые (для металлов) ее установил немец­кий ученый Георг Ом, поэтому зависимость силы тока от напря­жения носит название закона Ома. На участке цепи, изображенной на рисунке 109, ток направлен от точки 1 к точке 2. Разность потен­циалов (напряжение) на концах проводника равна: U = φ₁ - φ_2. Так как ток направлен слева направо, то напряженность электрического поля направлена в ту же сторону и φ₁ > φ₂

Согласно закону Ома для участка цепи сила тока прямо пропорцио­нальна приложенному напряжению U и обратно пропорциональна сопро­тивлению проводника R:

Закон Ома имеет очень простую форму, но доказать эксперименталь­но его справедливость довольно трудно. Дело в том, что разность по­тенциалов на участке металлическо­го проводника даже при большой силе тока мала, так как мало сопро­тивление проводника.

Электрометр, о котором шла речь, непригоден для измерения столь малых напряжений: его чув­ствительность слишком мала. Нужен несравненно более чувствительный прибор. Тогда, измеряя силу тока амперметром, а напряжение чув­ствительным электрометром, можно убедиться в том, что сила тока пря­мо пропорциональна напряжению. Применение же обычных приборов для измерения напряжения — вольт­метров — основано на использовании закона Ома.

Принцип устройства, вольтметра такой же, как и ампер­метра. Угол поворота стрелки прибо­ра пропорционален силе тока. Сила тока, проходящего по вольтметру, определяется напряжением между точками цепи, к которой он под­ключен. Поэтому, зная сопротивле­ние вольтметра, можно по силе тока определить напряжение. На практике прибор градуируют так, чтобы он сразу показывал напряжение в воль­тах.

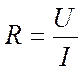
Сопротивление. Основная элек­трическая характеристика проводни­ка — сопротивление. От этой вели­чины зависит сила тока в провод­нике при заданном напряжении. Со­противление проводника представля­ет собой как бы меру противо­действия проводника установлению в нем электрического тока. С помощью закона Ома можно определить сопротивление проводника:

Для этого нужно измерить напря­жение и силу тока.

Сопротивление зависит от мате­риала проводника и его геометри­ческих размеров. Сопротивление про­водника длиной l с постоянной пло­щадью поперечного сечения S равно:

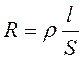где р — величина, зависящая от рода вещества и его состояния (от тем­пературы в первую очередь). Вели­чину р называют удельным сопро­тивлением проводника. Удельное со­противление численно равно сопро­тивлению проводника, имеющего форму куба с ребром 1 м, если ток направлен вдоль нормали к двум противоположным граням куба.

Единицу сопротивления провод­ника устанавливают на основе зако­на Ома и называют ее ом. Провод­ник имеет сопротивление 1 Ом, если при разности потенциалов 1 В сила тока в нем 1 А.

Единицей удельного сопротивле­ния является 1 Ом?м. Удельное со­противление металлов мало. Диэлектрики обладают очень большим удельным сопротивлением. В табли­це на форзаце приведены примеры значений удельного сопротивления некоторых веществ.

Значение закона Ома.

Закон Ома определяет силу тока в электриче­ской цепи при заданном напря­жении и известном сопротивлении. Он позволяет рассчитать тепловые, химические и магнитные действия тока, так как они зависят от силы тока. Из закона Ома вытекает, что замыкать обычную осветительную сеть проводником малого сопротив­ления опасно. Сила тока окажется настолько большой, что это может иметь тяжелые последствия.

Закон Ома — основа всей элект­ротехники постоянных токов. Формулу 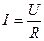— надо хорошо понять и твердо запомнить.

ЭЛЕКТРИЧЕСКИЕ ЦЕПИ. ПОСЛЕДОВАТЕЛЬНОЕ И ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЯ ПРОВОДНИКОВ

От источника тока энергия может быть передана по проводам к устрой­ствам, потребляющим энергию: Элек­трической лампе, радиоприемнику и др. Для этого составляют электри­ческие цепи различной сложности. Электрическая цепь состоит из источника энергии, устройств, по­требляющих электрическую энергию, соединительных проводов и выклю­чателей для замыкания цепи. Часто и электрическую цепь включают приборы, контролирующие силу тока и напряжение на различных участ­ках цепи, - амперметры и вольт­метры.

К наиболее простым и часто встречающимся соединениям провод­ников относятся последовательное и параллельное соединения.

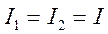
Последовательное соединение проводников.

При последовательном соединении электрическая цепь не имеет разветвлений. Все проводники включают в цепь поочередно друг за другом. На рисунке 1 показано последовательное соединение двух проводников 1 и 2, имеющих сопротивления R₁, и R₂. Это могут быть две лампы, две обмотки элект­родвигателя и др.

Сила тока в обоих проводниках одинакова, т. е. (1)

так как в проводниках электриче­ский заряд в случае постоянного тока не накапливается и через любое поперечное сечение проводника за определенное время проходит один и тот же заряд.

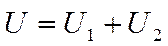
Напряжение на концах рассмат­риваемого участка цепи складывает­ся из напряжений на - первом и вто­ром проводниках:

Надо надеяться, что с доказатель­ством этого простого соотношения вы справитесь сами.

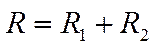
Применяя закон Ома для всего участка в целом и для участков с сопротивлениями R₁ и R₂, можно до­казать, что полное сопротивление всего участка цепи при последова­тельном соединении равно:

(2)

Это правило можно применить для любого числа последовательно соединенных проводников.

Напряжения на проводниках и их сопротивления при последователь­ном соединении связаны соотноше­нием:

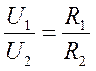(3)

Докажите это равенство.

Параллельное соединение про­водников.

На рисунке 2 показано параллельное соединение двух про­водников 1 и 2с сопротивлениями R₁ и R₂. В этом случае электриче­ский ток 1 разветвляется на две час­ти. Силу тока в первом и втором про­водниках обозначим через I₁ и I₂. Так как в точке а — разветвлении проводников (такую точку называют узлом) — электрический заряд не на­капливается, то заряд, поступающий в единицу времени в узел, равен заряду, уходящему из узла за это же время. Следовательно, I = I₁ + I₂

Напряжение U на концах про­водников, соединенных параллельно, одно и то же.

В осветительной сети поддержи­вается напряжение 220 или 127 В. На это напряжение рассчитаны при­боры, потребляющие электрическую энергию. Поэтому параллельное сое­динение — самый распространенный способ соединения различных потре­бителей. В этом случае выход из строя одного прибора не отражается на работе остальных, тогда как при последовательном соединении выход из строя одного прибора размы­кает цепь.

Применяя закон Ома для всего участка в целом и для участков с сопротивлениями R₁ и R ₂, можно доказать, что величина, обратная полному сопротивлению участка ab, равна сумме величин, обратных сопротивлениям отдельных провод­ников:

 (4)

Отсюда следует, что

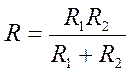(5)

Сила тока в каждом из провод­ников и сопротивления проводников при параллельном соединении свя­заны соотношением

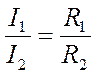
Различные проводники в цепи соединяются друг с другом после­довательно или параллельно. В пер­вом случае сила тока одинакова во всех проводниках, а во втором слу­чае одинаковы напряжения на про­водниках. Чаще всего к осветитель­ной сети различные потребители тока подключаются параллельно.

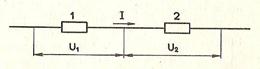Рис №1

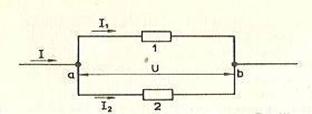Рис №2

ИЗМЕРЕНИЕ СИЛЫ ТОКА И НАПРЯЖЕНИЯ

Как измерить силу тока ампер­метром, а напряжение вольтметром, должен знать каждый.

Измерение силы тока.

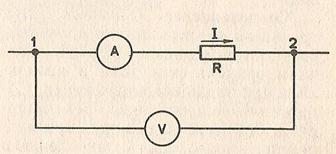
Для изме­рения силы тока в проводнике ам­перметр включают последовательно с этим проводником (рис. 1). Но нужно иметь в виду, что сам ампер­метр обладает некоторым сопротив­лением R_a. Поэтому сопротивление участка цепи с включенным ампер­метром увеличивается, и при неиз­менном напряжении сила тока умень­шается в соответствии с законом Ома. Чтобы амперметр оказывал как можно меньшее влияние на силу тока, измеряемую им, его сопротив­ление делают очень малым. Это нужно помнить и никогда не пытать­ся измерять силу тока в освети­тельной сети, подключая амперметр к розетке. Произойдет короткое за­мыкание; сила тока при малом со­противлении прибора достигнет столь большой величины, что обмотка ам­перметра сгорит.

Измерение напряжения.

Для того чтобы измерить напряжение на участке цепи с сопротивлением R, к нему параллельно подключают вольтметр. Напряжение на вольтметре совпа­дает с напряжением на участке цепи (рис. 2).

Если сопротивление вольтметра R_B, то после включения его в цепь сопротивление участка будет уже не R, а 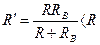. Из-за этого измеряемое напряжение на участ­ке цепи уменьшится. Для того чтобы вольтметр не вносил заметных иска­жений в измеряемое напряжение, его сопротивление должно быть большим по сравнению с сопротивлением участка цепи, на котором измеряется напряжение. Вольтметр можно вклю­чать в сеть без риска, что он сгорит, если только он рассчитан на напря­жение, превышающее напряжение сети.

Амперметр включают последова­тельно с проводником, в котором измеряют силу тока. Вольтметр включают параллельно проводнику, на котором измеряют напряжение.

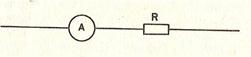Рис №1

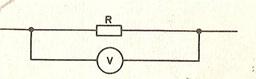Рис №2

РАБОТА И МОЩНОСТЬ ПОСТОЯННОГО ТОКА

Электрический ток получил такое широкое применение потому, что он несет с собой энергию. Эта энергия может быть превращена в любую форму.

При упорядоченном движении за­ряженных частиц в проводнике электрическое поле совершает ра­боту; ее принято называть работой тока. Сейчас мы напомним сведения о работе и мощности тока из курса физики VIII класса.

Работа тока.

Рассмотрим произ­вольный участок цепи. Это, может быть однородный проводник, напри­мер нить лампы накаливания, обмот­ка электродвигателя и др. Пусть за время t через поперечное сечение проводника проходит заряд q. Тогда электрическое поле совершит работу A = qU.

Так как сила тока 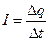, то эта работа равна:

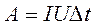(1)

Работа тока на участке цепи равна произведению силы тока, на­пряжения и времени, в течение ко­торого совершалась работа.

Согласно закону сохранения энергии эта работа должна быть рав­на изменению энергии рассматри­ваемого участка цепи. Поэтому энер­гия, выделяемая на данном участке цепи за время At, равна работе тока (см. формулу (1)).

В случае если на участке цепи не совершается механическая рабо­та и ток не производит химических действий, происходит только нагре­вание проводника. Нагретый про­водник отдает теплоту окружающим телам.

Нагревание проводника происхо­дит следующим образом. Электриче­ское поле ускоряет электроны. После столкновения с ионами кристалличе­ской решетки они передают ионам свою энергию. В результате энергия беспорядочного движения ионов око­ло положений равновесия возраста­ет. Это и означает увеличение внут­ренней энергии. Температура про­водника при этом повышается, и он начинает передавать теплоту окру­жающим телам. Спустя небольшое время после замыкания цепи процесс устанавливается, и температура пе­рестает изменяться со временем. К проводчику за счет работы элект­рического поля непрерывно поступа­ет энергия. Но его внутренняя энер­гия остается неизменной, так как проводник передает окружающим те­лам количество теплоты, равное ра­боте тока. Таким образом, формула (1) для работы тока определяет количество теплоты, передаваемое проводником другим телам.

Если в формуле (1) выразить либо напряжение через силу тока, либо силу тока через напряжение с помощью закона Ома для участка цепи, то получим три эквивалентные формулы:

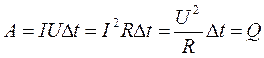(2)

Формулой A = I²R t удобно пользоваться для последовательного соединения проводников, так как сила тока в этом случае одинакова во всех проводниках. При парал­лельном соединении удобна формула 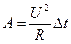, так как напряжение на всех проводниках одинаково.

Закон Джоуля — Ленца.

Закон, определяющий количество теплоты, которое выделяет проводник с то­ком в окружающую среду, был впервые установлен эксперименталь­но английским ученым Д. Джоу­лем (1818-1889) и русским ученым Э. X. Ленцем (1804-1865). Закон Джоуля — Ленца был сформулиро­ван следующим образом: количество теплоты, выделяемое проводником с током, равно произведению квад­рата силы тока, сопротивления про­водника и времени прохождения то­ка по проводнику:

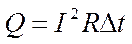(3)

Мы получили этот закон с по­мощью рассуждений, основанных на законе сохранения энергии. Формула (3) позволяет вычислить количе­ство теплоты, выделяемое на любом участке цепи, содержащем какие угодно проводники.

Мощность тока.

Любой электри­ческий прибор (лампа, электродвигатель) рассчитан на потребление определенной энергии в единицу вре­мени. Поэтому наряду с работой то­ка очень важное значение имеет по­нятие мощность тока. Мощность то­ка равна отношению работы тока за время t к этому интервалу времени.

Согласно этому определению

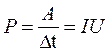(4)

Это выражение для мощности можно переписать в нескольких эквивалентных формах, если исполь­зовать закон Ома для участка цепи:

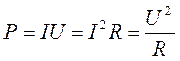
На большинстве приборов ука­зана потребляемая ими мощность.

Прохождение по проводнику электрического тока сопровождается выделением в нем энергии. Эта энер­гия определяется работой тока: про­изведением перенесенного заряда и напряжения на концах проводника.

ЭЛЕКТРОДВИЖУЩАЯ СИЛА.

Любой источник тока характеризуется электродвижущей силой, или ЭДС. Так, на круглой батарейке для карманного фонарика написано: 1,5 В. Что это значит?

Соедините проводником два ме­таллических шарика, несущих за­ряды противоположных знаков. Под влиянием электрического поля этих зарядов в проводнике возникает электрический ток (рис. 1). Но этот ток будет очень кратковремен­ным. Заряды быстро нейтрализуют­ся, потенциалы шариков станут одинаковыми, и электрическое поле ис­чезнет.

Сторонние силы.

Для того чтобы ток был постоянным, надо поддер­живать постоянное напряжение меж­ду шариками. Для этого необходимо устройство (источник тока), которое перемещало бы заряды от одного шарика к другому в направлении, противоположном направлению сил, действующих на эти заряды со сто­роны электрического поля шариков. В таком устройстве на заряды, кро­ме электрических сил, должны дей­ствовать силы не электростатического происхождения (рис. 2). Одно лишь электрическое поле заряжен­ных частиц (кулоновское поле) не способно поддерживать постоянный ток в цепи.

Любые силы, действующие на электрически заряженные частицы, за исключением сил электростати­ческого происхождения (т. е. кулоновских), называют сторонними си­лами.

Вывод о необходимости сторон­них сил для поддержания посто­янного тока в цепи станет еще оче­виднее, если обратиться к закону сохранения энергии. Электростатиче­ское поле потенциально. Работа это­го поля при перемещении заряжен­ных частиц вдоль замкнутой электри­ческой цепи равна нулю. Прохож­дение же тока по проводникам сопровождается выделением энер­гии — проводник нагревается. Сле­довательно, в любой цепи должен быть какой-то источник энергии, по­ставляющий ее в цепь. В нем, по­мимо кулоновских сил, обязательно должны действовать сторонние не­ потенциальные силы. Работа этих сил вдоль замкнутого контура долж­на быть отлична от нуля. Именно в процессе совершения работы этими силами заряженные частицы приобретают внутри источника тока энер­гию и отдают ее затем проводникам электрической цепи.

Сторонние силы приводят в дви­жение заряженные частицы внутри всех источников тока: в генераторах на электростанциях, в гальваниче­ских элементах, аккумуляторах и т.д.

При замыкании цепи создается электрическое поле во всех провод­никах цепи. Внутри источника тока заряды движутся под действием сторонних сил против кулоновских сил (электроны от положительно заряженного электрода к отрица­тельному), а во всей остальной цепи их приводит в движение электриче­ское поле (см. рис. 2).

Аналогия между электрическим током и течением жидкости.

Чтобы лучше понять механизм возникнове­ния тока, обратимся к сходству меж­ду электрическим током в провод­нике и течением жидкости по трубам.

На любом участке горизонталь­ной трубы жидкость течет за счет разности давлений на концах участ­ка. Жидкость перемещается в сторо­ну уменьшения давления. Но сила давления в жидкости — это вид сил упругости, которые являются потен­циальными, подобно кулоновским силам. Поэтому работа этих сил на замкнутом пути равна нулю и одни эти силы не способны вызвать длительную циркуляцию жидкости по трубам. Течение жидкости сопро­вождается потерями энергии вслед­ствие действия сил трения. Для цир­куляции воды необходим насос.

Поршень этого насоса действует на частички жидкости и создает по­стоянную разность давлений на вхо­де и выходе насоса (рис. 3). Благодаря этому жидкость течет по трубе. Насос подобен источнику тока, а роль сторонних сил играет сила, действующая на воду со стороны движущегося поршня. Внутри на­соса жидкость течет от участков с меньшим давлением к участкам с большим давлением. Разность дав­лений аналогична напряжению.

Природа сторонних сил.

Природа сторонних сил может быть разнооб­разной. В генераторах электростанций сторонняя сила — это сила, дей­ствующая со стороны магнитного поля на электроны в движущемся проводнике. Об этом кратко гово­рилось в курсе физики VIII класса.

В гальваническом элементе, на­пример элементе Вольта, действуют химические силы. Элемент Вольта состоит из цинкового и медного электродов, помещенных в раствор серной кислоты. Химические силы вызывают растворение цинка в кис­лоте. В раствор переходят положи­тельно заряженные ионы цинка, а сам цинковый электрод при этом заряжается отрицательно. (Медь очень мало растворяется в серной - кислоте.) Между цинковым и мед­ным электродами появляется раз­ность потенциалов, которая обуслов­ливает ток в замкнутой электриче­ской цепи.

Электродвижущая сила.

Дейст­вие сторонних сил характеризуется важной физической величиной, на­зываемой электродвижущей силой (сокращенно ЭДС).

Электродви­жущая сила в замкнутом контуре представляет собой отношение рабо­ты сторонних сил при перемещении заряда вдоль контура к заряду:

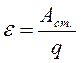(1)

Электродвижущую силу выража­ют в вольтах.

Можно говорить об электродви­жущей силе на любом участке цепи. Это удельная работа сторонних сил (работа по перемещению единич­ного заряда) не во всем контуре, а только на данном участке. Электро­движущая сила гальванического эле­мента есть работа сторонних сил при перемещении единичного положи­тельного заряда внутри элемента от одного полюса к другому. Работа сторонних сил не может быть вы­ражена через разность потенциалов, так как сторонние силы не потенциальные и их работа зависит от формы траектории. Так, например, работа сторонних сил при переме­щении заряда между клеммами ис­точника тока вне самого источника равна нулю.

Теперь вы знаете, что такое ЭДС. Если на батарейке написано 1,5 В, то это означает, что сторонние силы (химические в данном случае) совер­шают работу 1,5 Дж при переме­щении заряда в 1 Кл от одного полюса батарейки к другому. Постоянный ток не может существовать в замкнутой цепи, если в ней не действуют сторонние силы, т. е. нет ЭДС

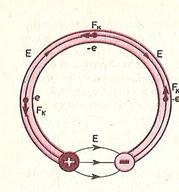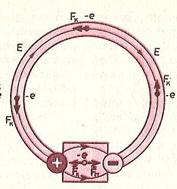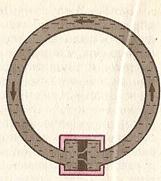Рис №1 Рис №2 Рис №3

ЗАКОН ОМА ДЛЯ ПОЛНОЙ ЦЕПИ

Электродвижущая сила опреде­ляет силу тока в замкнутой электри­ческой цепи с известным сопротив­лением.

Спомощью закона сохранения энергии найдем зависимость силы тока от ЭДС и сопротивления.

Рассмотрим простейшую полную (замкнутую) цепь, состоящую из источника тока (гальванического элемента, аккумулятора или гене­ратора) и резистора сопротивле­нием R (рис. 1). Источник тока имеет ЭДС εи сопротивление r. Сопротивление источника часто на­зывают внутренним сопротивлением в отличие от внешнего сопротивле­ния R цепи. В генераторе r — это сопротивление обмоток, а в гальва­ническом элементе — сопротивление раствора электролита и электродов.

Закон Ома для замкнутой цепи связывает силу тока в цепи, ЭДС и полное сопротивление R + r цепи. Эта связь может быть установлена теоретически, если использовать за­кон сохранения энергии и закон Джоуля — Ленца.

Пусть за время t через попе­речное сечение проводника пройдет электрический заряд q. Тогда рабо­ту сторонних сил при перемещении заряда?qможно записать так: А_ст = ε · q. Согласно определению силы тока q = It. Поэтому

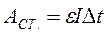(1)

При совершении этой работы на внутреннем и внешнем участках цепи, сопротивления которых r и R, выделяется некоторое количество теплоты. По закону Джоуля — Лен­ца оно равно:

Q = I²R · t + I²r · t. (2)

Согласно закону сохранения энергии A = Q. Приравнивая (1) и (2), получим:

ε = IR + Ir (3)

Произведение силы тока и сопро­тивления участка цепи часто назы­вают падением напряжения на этом участке. Таким образом, ЭДС равна сумме падений напряжений на внут­реннем и внешнем участках замкну­той цепи.

Обычно закон Ома для замкну­той цепи записывают в форме

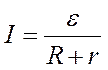(4)