Гармонические колебания — колебания, при которых колеблющаяся величина 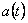 изменяется со временем по закону синуса или косинуса:
изменяется со временем по закону синуса или косинуса:
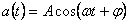 , где
, где 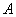 — амплитуда колебаний,
— амплитуда колебаний, 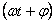 — фаза,
— фаза, 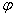 — начальная фаза в момент
— начальная фаза в момент 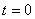 ,
,
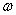 — круговая (циклическая) частота. Гармонические колебания возникают, когда сила, возвращающая тело в положение равновесия, пропорциональна величине отклонения от равновесия.
— круговая (циклическая) частота. Гармонические колебания возникают, когда сила, возвращающая тело в положение равновесия, пропорциональна величине отклонения от равновесия.
В этом случае уравнение динамики принимает вид однородного дифференциального уравнения второго порядка, решением которого является гармоническая функция (синуса или косинуса):
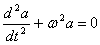 .
.
Пружинный маятник — груз массой 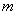 , подвешенный на абсолютно упругой пружине и совершающий гармонические колебания под действием упругой силы
, подвешенный на абсолютно упругой пружине и совершающий гармонические колебания под действием упругой силы
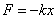 .
.
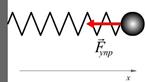
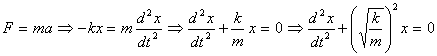 .
.
Циклическая частота колебаний пружинного маятника 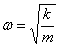 .
.
Период колебаний математического маятника 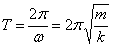 .
.
Частота колебаний математического маятника 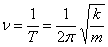 .
.
Математический маятник — материальная точка массой 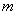 , подвешенная на нерастяжимой невесомой нити длиной
, подвешенная на нерастяжимой невесомой нити длиной 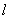 и колеблющаяся под действием силы тяжести.
и колеблющаяся под действием силы тяжести.
|
|
|
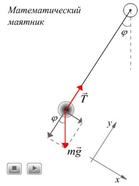
По второму закону Ньютона:
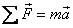 ,
, 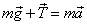
В проекциях на координатные оси:
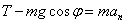 ,
, 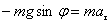 .
.
Связь тангенциального ускорения 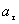 и угла поворота маятника
и угла поворота маятника 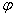 :
:
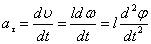 .
.
Уравнение в проекциях на ось x принимает вид:
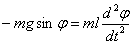 .
.
При малых значениях угла 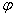
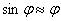 .
.
Таким образом,
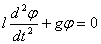 или
или 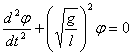 .
.
Циклическая частота колебаний математического маятника 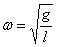 .
.
Период колебаний математического маятника 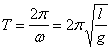 .
.
Частота колебаний математического маятника 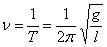 .
.
Физический маятник — твердое тело, совершающее под действием силы тяжести колебания вокруг неподвижной горизонтальной оси, не проходящей через центр масс тела.
(В однородном поле силы тяжести центр масс тела совпадает с центром тяжести).
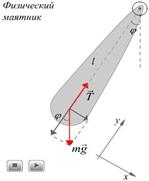
Основное уравнение динамики твердого тела:
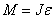
Момент силы тяжести
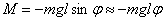 .
.
Угловое ускорение
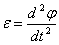 .
.
Уравнение динамики физического маятника принимает вид:
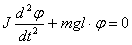 или
или 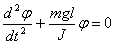 ,
,
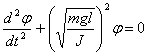 .
.
Циклическая частота колебаний физического маятника 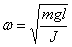 .
.
Период колебаний физического маятника 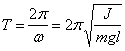 .
.
Частота колебаний физического маятника 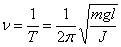 .
.
 2015-07-14
2015-07-14 7144
7144
