Формула Максвелла для относительных скоростей

Для решения многих задач удобно использовать формулу Максвелла, где скорость выражена в относительных единицах.

Относительную скорость обозначим через u:

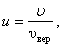(2.3.12)

где 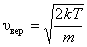. Тогда из (2.3.3), получим

.

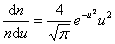(2.3.13)

Это уравнение универсальное. В таком виде функция распределения не зависит ни от рода газа, ни от температуры.

На рисунке 2.7 показано максвелловское распределение частиц f (υ), имеющих скорости от υ до υ+dυ. За единицу скорости здесь взята наиболее вероятная скорость.

Полезно знать, что .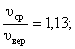

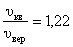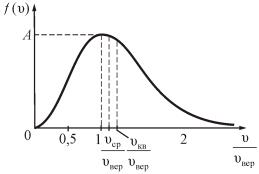
Рис. 2.7